Question

【题目】在平面内， ⊥ ，| |=| |=2， = + ，若| |＜1，则| |的取值范围是 ．

Answer 1

【答案】（ ，2 ]
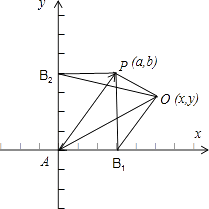
【解析】解：根据题意知，A、B1、P、B2构成一个矩形AB1PB2 ，
以AB1 ， AB2所在直线为坐标轴建立直角坐标系，如图所示；
设|AB1|=a，|AB2|=b，点O的坐标为（x，y），则点P的坐标为（a，b）；
B1（a，0），B2（0，b），
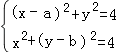由| |=| |=2，得 ，则 ；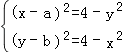
∵| |＜1，∴（x﹣a）2+（y﹣b）2＜1，
∴4﹣y2+4﹣x2＜1，
∴x2+y2＞7；①
又∵（x﹣a）2+y2=4，
∴y2=4﹣（x﹣a）2≤4，
∴y2≤4，
同理x2≤4，
∴x2+y2≤8；②
由①②知7＜x2+y2≤8，
∵| |= ，
∴ ＜| |≤2 ．
所以答案是：（ ，2 ]