题目内容
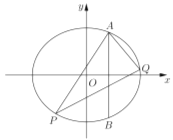
【题目】在平面直角坐标系xOy中，曲线C的参数方程为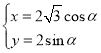
，其中
为参数，在以坐标原点O为极点，x轴的正半轴为极轴的极坐标系中，点P的极坐标为
，直线l的极坐标方程为
.
（1）求曲线C的普通方程与直线l的直角坐标方程；
（2）若Q是曲线C上的动点，M为线段PQ的中点，求点M到直线l的距离的最大值.
【答案】（1）曲线C：
，直线l：
；（2）
.
【解析】
（1）将参数方程变为
，两式平方相加即可；利用两角差的正弦公式展开，再根据
，代换即可求解.
（2）设
，将点P的极坐标化为直角坐标为
，利用中点坐标公式可得
，代入点到直线的距离公式，根据三角函数的性质即可求解.
（1）消去参数a，可得曲线C的普通方程为.
可化为
，
由
，可得直线l的直角坐标方程为.
（2）设，
将点P的极坐标化为直角坐标为，
因为M为线段PQ的中点，所以，
所以点M到直线l的距离
，
当且仅当
，即
时取等号，
所以点M到直线l的距离的最大值为.
练习册系列答案
阅读快车系列答案
相关题目
