题目内容
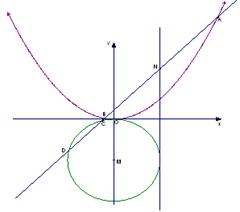
如图,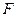 是抛物线
是抛物线 的焦点,
的焦点, 为准线与
为准线与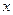 轴的交点,直线
轴的交点,直线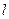 经过点
经过点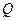 .
.
(Ⅰ)直线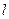 与抛物线有唯一公共点,求
与抛物线有唯一公共点,求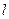 的方程;
的方程;
(Ⅱ)直线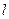 与抛物线交于
与抛物线交于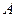 、
、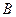 两点记
两点记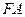 、
、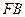 的斜率分别为
的斜率分别为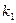 ,
,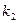 .(1)求证:
.(1)求证: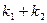 为定值;
为定值;
(2)若点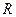 在线段
在线段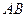 上,且满足
上,且满足
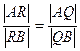 ,求点
,求点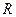 的轨迹方程.
的轨迹方程.
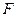 是抛物线
是抛物线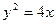 的焦点,
的焦点,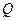 为准线与
为准线与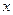 轴的交点,直线
轴的交点,直线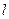 经过点
经过点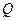 .
. (Ⅰ)直线
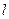 与抛物线有唯一公共点,求
与抛物线有唯一公共点,求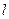 的方程;
的方程;
|
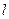 与抛物线交于
与抛物线交于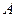 、
、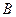 两点记
两点记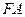 、
、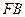 的斜率分别为
的斜率分别为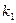 ,
,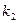 .(1)求证:
.(1)求证: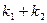 为定值;
为定值; (2)若点
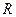 在线段
在线段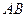 上,且满足
上,且满足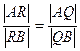 ,求点
,求点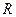 的轨迹方程.
的轨迹方程.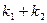 为定值
为定值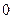 .,轨迹方程为
.,轨迹方程为 .
.解:由已知得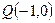 ,显然直线
,显然直线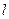 的斜率存在。设直线
的斜率存在。设直线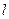 的斜率为
的斜率为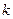 ,则
,则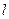 的方程为
的方程为
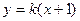 ,代入抛物线方程得
,代入抛物线方程得
⑴ 若 ,令
,令 ,此时
,此时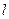 的方程为
的方程为
即 或
或 。若
。若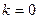 ,方程有唯一解
,方程有唯一解 ,此时
,此时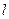 的方程为
的方程为 .
.
综上,所求直线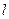 的方程为:
的方程为: 或
或 或
或 .
.
⑵ 显然 ,记
,记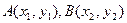 ,则
,则
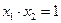
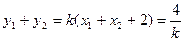 ,
, 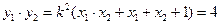
①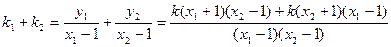
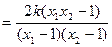
∵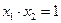
 ∴
∴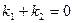 即
即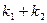 为定值
为定值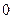 .
.
②设动点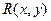 ,∵
,∵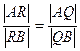 ,
,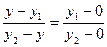 ∴
∴

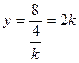 ∴
∴
令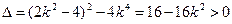 且
且
∴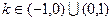 ∴
∴ 
综上,点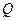 的轨迹方程为
的轨迹方程为 .
.
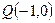 ,显然直线
,显然直线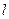 的斜率存在。设直线
的斜率存在。设直线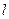 的斜率为
的斜率为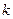 ,则
,则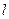 的方程为
的方程为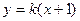 ,代入抛物线方程得
,代入抛物线方程得
⑴ 若
 ,令
,令 ,此时
,此时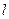 的方程为
的方程为
即
 或
或 。若
。若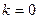 ,方程有唯一解
,方程有唯一解 ,此时
,此时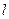 的方程为
的方程为 .
.综上,所求直线
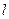 的方程为:
的方程为: 或
或 或
或 .
.⑵ 显然
 ,记
,记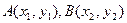 ,则
,则
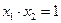
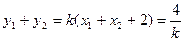 ,
, 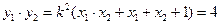
①
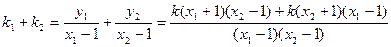
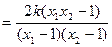
∵
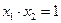
 ∴
∴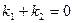 即
即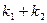 为定值
为定值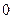 .
.②设动点
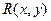 ,∵
,∵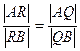 ,
,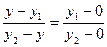 ∴
∴

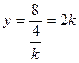 ∴
∴
令
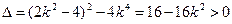 且
且
∴
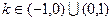 ∴
∴ 
综上,点
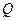 的轨迹方程为
的轨迹方程为 .
.
练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目

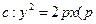 >0)上有两动点A、B(AB不垂直
>0)上有两动点A、B(AB不垂直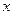 轴),F为焦点,且
轴),F为焦点,且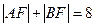 ,又线段AB的垂直平分线经过定点Q(6,0),求抛物线方程。
,又线段AB的垂直平分线经过定点Q(6,0),求抛物线方程。
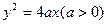 的焦点为F,以点
的焦点为F,以点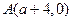 为圆心,|AF|为半径的圆在x轴的上方与抛物线交于M、N两点。
为圆心,|AF|为半径的圆在x轴的上方与抛物线交于M、N两点。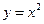 上求一点,使该点到直线
上求一点,使该点到直线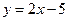 的距离最小,并求最小值.
的距离最小,并求最小值.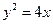 上一点
上一点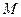 到焦点的距离为3,则点
到焦点的距离为3,则点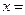 .
.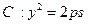 (p>0)
(p>0)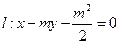 上。
上。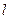 与抛物线C交于A、B,△A
与抛物线C交于A、B,△A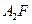 ,△
,△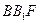 的重心分别为G,H
的重心分别为G,H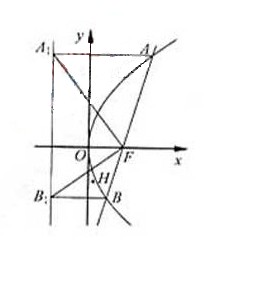
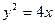 上的不同两点,F为抛物线C的焦点,若
上的不同两点,F为抛物线C的焦点,若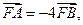 则直线AB的斜率为 ( )
则直线AB的斜率为 ( )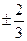 B.
B.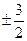 C.
C.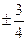 D.
D.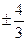
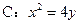 ,圆
,圆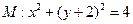 ,
,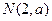 (其中
(其中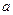 为常数)是
为常数)是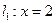 上的点,倾斜角为锐角
上的点,倾斜角为锐角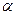 的直线
的直线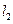 过点
过点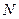 且与抛物线C交于两点A、B,与圆M交于C、D两点.
且与抛物线C交于两点A、B,与圆M交于C、D两点.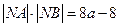 ,且
,且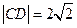 ,求
,求