题目内容
(本小题14分)已知数列 为等差数列,
为等差数列, ,
, ,数列
,数列 的前
的前 项和为
项和为 ,且有
,且有
(1)求 、
、 的通项公式;
的通项公式;
(2)若 ,
, 的前
的前 项和为
项和为 ,求
,求 ;
;
(3)试比较 与
与 的大小,并说明理由.
的大小,并说明理由.
解:(1)∵ 是等差数列,且
是等差数列,且 ,
, ,设公差为
,设公差为 。
。
∴ , 解得
, 解得
∴ (
( ) …2分
) …2分
在 中,∵
中,∵
当 时,
时, ,∴
,∴
当 时,由
时,由 及
及 可得
可得 ,∴
,∴
∴ 是首项为1公比为2的等比数列
是首项为1公比为2的等比数列
∴ (
( ) …4分
) …4分
(2)
 ①
① ②
②
①-②得 



∴ (
( ) …8分
) …8分
(3)

 …9分
…9分
令 ,则
,则
∵ 在
在 是减函数,又
是减函数,又
∴ 时,
时,
∴ 时,
时, 是减函数.
是减函数.
又
∴ 时,
时,
∴ 时,
时, …13分
…13分
∴ 时,
时,
∴ 时,
时, …14分
…14分
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
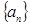 满足
满足 ,且
,且 是
是 ,
, 的等差中项.
的等差中项. ,
, ,求使
,求使  成立的正整数
成立的正整数 的最小值.
的最小值. ,设
,设 。
。 图象上任意一点
图象上任意一点 为切点的切线的斜率
为切点的切线的斜率 恒成立,求实数
恒成立,求实数 的最小值。
的最小值。 ,使得函数
,使得函数 的图象与
的图象与 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出 的图像与函数
的图像与函数 的图像关于点
的图像关于点 对称
对称 ,
, 在区间
在区间 上的值不小于6,求实数a的取值范围.
上的值不小于6,求实数a的取值范围. 的图像在[a,b]上连续不断,定义:
的图像在[a,b]上连续不断,定义: ,
, ,其中
,其中 表示函数
表示函数 在D上的最小值,
在D上的最小值, 表示函数
表示函数 对任意的
对任意的 成立,则称函数
成立,则称函数 上的“k阶收缩函数”
上的“k阶收缩函数” ,试写出
,试写出 ,
, 的表达式;
的表达式; 试判断
试判断 ,函数
,函数 是[0,b]上的2阶收缩函数,求b的取值范围
是[0,b]上的2阶收缩函数,求b的取值范围