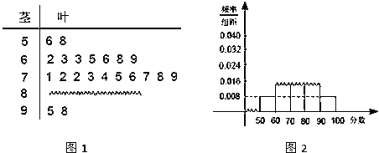题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,若
时,若![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的最小值.
的最小值.
【答案】(1)![]() 在
在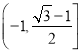 上单调递减,在
上单调递减,在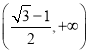 上单调递增.(2)
上单调递增.(2)![]()
【解析】
(1)按绝对值定义分类讨论后求导数(在定义域内),确定导数的正负,得单调区间;
(2)不等式变形为![]() ,设
,设![]() .分类
.分类![]() ,用特例说明不等式不恒成立,
,用特例说明不等式不恒成立,![]() 时,求导数,确定
时,求导数,确定![]() 的单调性,最值得结论.
的单调性,最值得结论.
(1)当![]() 时,
时,![]()
当![]() 时,
时,![]() ,
,
![]() ,
,
∴![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时则
时则![]() 在
在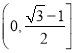 上单调递减,在
上单调递减,在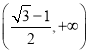 上单调递增.
上单调递增.
![]() ,
,
则![]() 在
在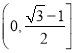 上单调递减,在
上单调递减,在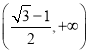 上单调递增.
上单调递增.
综上,![]() 在
在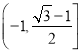 上单调递减,在
上单调递减,在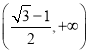 上单调递增.
上单调递增.
(2)当![]() 时,
时,![]() ,
,
则![]() 对
对![]() 恒成立.
恒成立.
即![]() ,设
,设![]() .
.
①当![]() 时,
时,![]() ,不合题意,舍去;
,不合题意,舍去;
②当![]() 时,
时,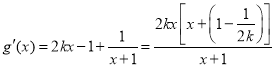 .
.
令![]() ,得
,得![]() ,
,![]() .
.
i)当![]() 时,
时,![]() ,
,![]() 在
在![]() 上恒成立,
上恒成立,
则![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,成立.
,成立.
ii)当![]() 时,
时,![]() ,对
,对![]() ,
,![]() ,
,![]() ,
,
不合题意,舍去.
综上,![]() 的最小值为
的最小值为![]() .
.

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】2019年安庆市在大力推进城市环境、人文精神建设的过程中,居民生活垃圾分类逐渐形成意识.有关部门为宣传垃圾分类知识,面向该市市民进行了一次“垃圾分类知识"的网络问卷调查,每位市民仅有一次参与机会,通过抽样,得到参与问卷调查中的1000人的得分数据,其频率分布直方图如图:
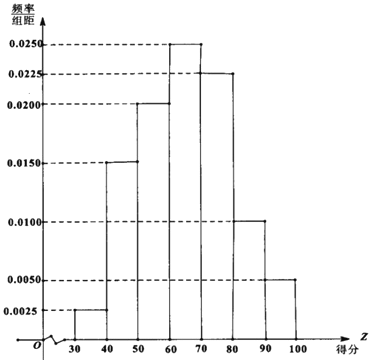
(1)由频率分布直方图可以认为,此次问卷调查的得分Z服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组数据用该区间的中点值作代表),利用该正态分布,求P(
近似为这1000人得分的平均值(同一组数据用该区间的中点值作代表),利用该正态分布,求P(![]() );
);
(2)在(1)的条件下,有关部门为此次参加问卷调查的市民制定如下奖励方案:
(i)得分不低于![]() 可获赠2次随机话费,得分低于
可获赠2次随机话费,得分低于![]() 则只有1次:
则只有1次:
(ii)每次赠送的随机话费和对应概率如下:
赠送话费(单位:元) | 10 | 20 |
概率 |
|
|
现有一位市民要参加此次问卷调查,记X(单位:元)为该市民参加问卷调查获赠的话费,求X的分布列.附:![]() ,若
,若![]() ,则
,则![]() ,
,![]() .
.
【题目】秉承“绿水青山就是金山银山”的发展理念,某市环保部门通过制定评分标准,先对本市的企业进行评估,评出四个等级,并根据等级给予相应的奖惩,如下表所示:
评估得分 |
|
|
|
|
评定等级 | 不合格 | 合格 | 良好 | 优秀 |
奖励(万元) |
|
|
|
|
环保部门对企业评估完成后,随机抽取了![]() 家企业的评估得分(
家企业的评估得分(![]() 分)为样本,得到如下频率分布表:
分)为样本,得到如下频率分布表:
评估得分 |
|
|
|
|
|
|
频率 |
|
|
|
|
|
|
其中![]() 、
、![]() 表示模糊不清的两个数字,但知道样本评估得分的平均数是
表示模糊不清的两个数字,但知道样本评估得分的平均数是![]() .
.
(1)现从样本外的数百个企业评估得分中随机抽取![]() 个,若以样本中频率为概率,求该家企业的奖励不少于
个,若以样本中频率为概率,求该家企业的奖励不少于![]() 万元的概率;
万元的概率;
(2)现从样本“不合格”、“合格”、“良好”三个等级中,按分层抽样的方法抽取![]() 家企业,再从这
家企业,再从这![]() 家企业随机抽取
家企业随机抽取![]() 家,求这两家企业所获奖励之和不少于
家,求这两家企业所获奖励之和不少于![]() 万元的概率.
万元的概率.
【题目】某单位准备购买三台设备,型号分别为![]() 已知这三台设备均使用同一种易耗品,提供设备的商家规定:可以在购买设备的同时购买该易耗品,每件易耗品的价格为100元,也可以在设备使用过程中,随时单独购买易耗品,每件易耗品的价格为200元.为了决策在购买设备时应购买的易耗品的件数.该单位调查了这三种型号的设备各60台,调査每台设备在一个月中使用的易耗品的件数,并得到统计表如下所示.
已知这三台设备均使用同一种易耗品,提供设备的商家规定:可以在购买设备的同时购买该易耗品,每件易耗品的价格为100元,也可以在设备使用过程中,随时单独购买易耗品,每件易耗品的价格为200元.为了决策在购买设备时应购买的易耗品的件数.该单位调查了这三种型号的设备各60台,调査每台设备在一个月中使用的易耗品的件数,并得到统计表如下所示.
每台设备一个月中使用的易耗品的件数 | 6 | 7 | 8 | |
型号A | 30 | 30 | 0 | |
频数 | 型号B | 20 | 30 | 10 |
型号C | 0 | 45 | 15 | |
将调查的每种型号的设备的频率视为概率,各台设备在易耗品的使用上相互独立.
(1)求该单位一个月中![]() 三台设备使用的易耗品总数超过21件的概率;
三台设备使用的易耗品总数超过21件的概率;
(2)以该单位一个月购买易耗品所需总费用的期望值为决策依据,该单位在购买设备时应同时购买20件还是21件易耗品?