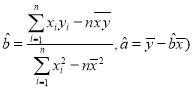题目内容
【题目】某单位准备购买三台设备，型号分别为
已知这三台设备均使用同一种易耗品，提供设备的商家规定：可以在购买设备的同时购买该易耗品，每件易耗品的价格为100元，也可以在设备使用过程中，随时单独购买易耗品，每件易耗品的价格为200元.为了决策在购买设备时应购买的易耗品的件数.该单位调查了这三种型号的设备各60台，调査每台设备在一个月中使用的易耗品的件数，并得到统计表如下所示.
每台设备一个月中使用的易耗品的件数 | 6 | 7 | 8 | |
型号A | 30 | 30 | 0 | |
频数 | 型号B | 20 | 30 | 10 |
型号C | 0 | 45 | 15 | |
将调查的每种型号的设备的频率视为概率，各台设备在易耗品的使用上相互独立.
（1）求该单位一个月中三台设备使用的易耗品总数超过21件的概率；
（2）以该单位一个月购买易耗品所需总费用的期望值为决策依据，该单位在购买设备时应同时购买20件还是21件易耗品？
【答案】（1）
（2）应该购买21件易耗品
【解析】
（1）由统计表中数据可得型号分别为
在一个月使用易耗品的件数为6,7,8时的概率,设该单位三台设备一个月中使用易耗品的件数总数为X,则
,利用独立事件概率公式进而求解即可；
（2）由题可得X所有可能的取值为
,即可求得对应的概率,再分别讨论该单位在购买设备时应同时购买20件易耗品和21件易耗品时总费用的可能取值及期望,即可分析求解.
（1）由题中的表格可知
A型号的设备一个月使用易耗品的件数为6和7的频率均为
；
B型号的设备一个月使用易耗品的件数为6,7,8的频率分别为
；
C型号的设备一个月使用易耗品的件数为7和8的频率分别为
；
设该单位一个月中三台设备使用易耗品的件数分别为
,则
,
,
,
设该单位三台设备一个月中使用易耗品的件数总数为X,
则
而
,
,
故
,
即该单位一个月中三台设备使用的易耗品总数超过21件的概率为.
（2）以题意知,X所有可能的取值为
；
；
；
由（1）知,
,
若该单位在购买设备的同时购买了20件易耗品,设该单位一个月中购买易耗品所需的总费用为
元,则的所有可能取值为
,
；
；
；
；
；
若该单位在肋买设备的同时购买了21件易耗品,设该单位一个月中购买易耗品所需的总费用为
元,则的所有可能取值为
,
；
；
；
；
,所以该单位在购买设备时应该购买21件易耗品
优生乐园系列答案
新编小学单元自测题系列答案
【题目】下表是某公司2018年5~12月份研发费用（百万元）和产品销量（万台）的具体数据：
月 份 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
研发费用（百万元） | 2 | 3 | 6 | 10 | 21 | 13 | 15 | 18 |
产品销量（万台） | 1 | 1 | 2 | 2.5 | 6 | 3.5 | 3.5 | 4.5 |
（Ⅰ）根据数据可知
与
之间存在线性相关关系，求出与的线性回归方程（系数精确到0.01）；
（Ⅱ）该公司制定了如下奖励制度：以
（单位：万台）表示日销售，当
时，每位员工每日奖励200元；当
时，每位员工每日奖励300元；当
时，每位员工每日奖励400元.现已知该公司某月份日销售（万台）服从正态分布
（其中
是2018年5-12月产品销售平均数的二十分之一），请你估计每位员工该月（按30天计算）获得奖励金额总数大约多少元.
参考数据：
，
，
，
，
参考公式：相关系数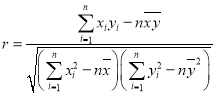
，其回归直线
中的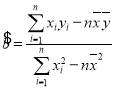
，若随机变量服从正态分布
，则
，
.