题目内容
【题目】已知正项数列![]() 为等比数列,等差数列
为等比数列,等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足:
,且满足:
![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)设![]() ,求
,求![]() ;
;
(3)设 ,问是否存在正整数
,问是否存在正整数![]() ,使得
,使得![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)借助题设条件运用等差数列的有关知识建立方程组求解;(2)借助题设运用错位相减法求和;(3)依据题设运用分类整合思想分析推证和探求.
试题解析:
(1)因为数列![]() 为等差数列,且
为等差数列,且![]() ,
,
即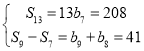 ,解得
,解得![]() ,公差为3,.............2分
,公差为3,.............2分
所以![]() ,得
,得![]() ..............3分
..............3分
又![]() ,
,
所以![]() ....................5分
....................5分
(2)![]() ,.........①
,.........①
则![]() ,..............②
,..............②
将①—②得:
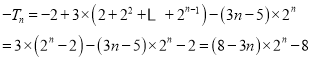
所以![]() ...................8分
...................8分
(3)因为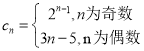 ,
,
当![]() 时,
时,![]() ,不等,...........9分
,不等,...........9分
当![]() 时,
时,![]() ,
,
![]() 成立,...............10分
成立,...............10分
当![]() 且为奇数时,
且为奇数时,![]() 为偶数,
为偶数,![]() 为奇数,
为奇数,
所以![]() 为偶数,
为偶数,![]() 为奇数,不成立,.............12分
为奇数,不成立,.............12分
当![]() ,且
,且![]() 为偶数时,若
为偶数时,若![]() ,
,
即![]() ,..................13分
,..................13分
得![]() .............(*)
.............(*)
因为![]() ,所以(*)不成立.......15分
,所以(*)不成立.......15分
综上得![]() ............................16分
............................16分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目