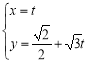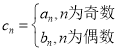题目内容
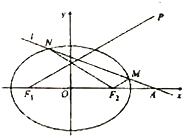
【题目】如图所示,已知圆![]() 的圆心在直线
的圆心在直线![]() 上,且该圆存在两点关于直线
上,且该圆存在两点关于直线![]() 对称,又圆
对称,又圆![]() 与直线
与直线![]() 相切,过点
相切,过点![]() 的动直线
的动直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,
两点,![]() 是
是![]() 的中点,直线
的中点,直线![]() 与
与![]() 相交于点
相交于点![]() .
.
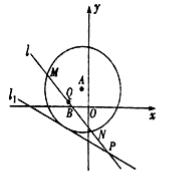
(1)求圆![]() 的方程;
的方程;
(2)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)![]() 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)是,
;(3)是,![]() .
.
【解析】
试题分析:(1)借助题设条件构建方程组求解;(2)借助题设建立方程组求解;(3)运用向量的坐标形式的运算推证求解.
试题解析:
(1)由圆存在两点关于直线![]() 对称知圆心
对称知圆心![]() 在直线
在直线![]() 上,
上,
由![]() 得
得![]() .
.
设圆![]() 的半径为
的半径为![]() ,因为圆
,因为圆![]() 与直线
与直线![]() 相切,
相切,
所以![]() .
.
所以圆![]() 的方程为
的方程为![]() .
.
(2)当直线![]() 与
与![]() 轴垂直时,易知
轴垂直时,易知![]() 符合题意..
符合题意..
当直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为
的方程为![]() ,
,
即![]() 连接
连接![]() ,则
,则![]() ,
,
∵![]() ,∴
,∴![]() ,
,
由![]() ,得
,得![]()
∴直线![]() 的方程为
的方程为![]() .
.
∴所求直线![]() 的方程为
的方程为![]() 或
或![]() .
.
(3)∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
当直线![]() 与
与![]() 轴垂直时,得
轴垂直时,得![]() ,则
,则![]() ,又
,又![]() ,
,
∴![]()
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
由![]() ,解得
,解得![]() ,∴
,∴![]() ,
,
∴![]()
综上所述,![]() 是定值,且为-10.
是定值,且为-10.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目