题目内容
已知![]() 是数列
是数列![]() 的前n项和,
的前n项和,![]() 满足关系式
满足关系式![]() ,
,![]()
(n≥2,n为正整数).
(1)令![]() ,证明:数列
,证明:数列![]() 是等差数列;
是等差数列;
(2)求数列![]() 的通项公式;
的通项公式;
(3)对于数列![]() ,若存在常数M>0,对任意的
,若存在常数M>0,对任意的![]() ,恒有
,恒有
![]() ≤M成立,称数列
≤M成立,称数列![]() 为“差绝对和有界数列”,
为“差绝对和有界数列”,
证明:数列![]() 为“差绝对和有界数列”.
为“差绝对和有界数列”.
(1) 见解析 (2)![]() (3)见解析
(3)见解析
解析:
(1)当![]() 时,
时,![]() ,
,![]()
![]()
所以 ![]() ,
,
即 ![]() ,
,
所以 ![]()
即![]() ,
, ![]()
又![]()
所以, ![]() ,
,![]()
即![]() 为等比数列
为等比数列
(2)![]()
![]()
![]()
(3)由于 ![]()
![]() (求和3分)
(求和3分)
所以![]() 恒成立,即
恒成立,即![]() 为“差绝对和有界数列”。
为“差绝对和有界数列”。

练习册系列答案
相关题目
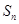 是数列
是数列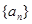 的前n项和,
的前n项和,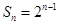 ,则
,则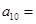 ( )
( )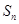 是数列{
是数列{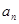 }的前n项和,
}的前n项和,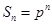 ,那么数列{
,那么数列{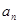 }中,
}中,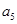 =162,公比q=3,前n项和
=162,公比q=3,前n项和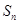 =242,求首项
=242,求首项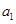 和项数n的值.
和项数n的值.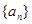 的前n项和,
的前n项和,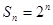 ,求
,求 是数列{
是数列{ }的前n项和,并且
}的前n项和,并且 =1,对任意正整数n,
=1,对任意正整数n, ;设
;设 ).(I)证明数列
).(I)证明数列 是等比数列,并求
是等比数列,并求 的前n项和,求
的前n项和,求 .
.