题目内容

如图,直角梯形ABDC，AB∥CD，AB＞CD，S是直角梯形ABDC所在平面外的一点，画出平面SBD和平面SAC的交线.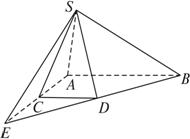

 

思路解析：点S是平面SBD和平面SAC的一个公共点，即点S在交线上.要找到两平面的交线，只需再找到一个公共点即可.

解：由于AB＞CD，则分别延长AC和BD交于点E，如右图所示.

∵E∈AC,AC平面SAC，∴E∈平面SAC.

同理,可证E∈平面SBD.∴点E在平面SBD和平面SAC的交线上.连结SE，则直线SE是面SBD和面SAC的交线.

练习册系列答案
相关题目
如右图，在直角梯形ABCD中，∠B=90°，DC∥AB，BC=CD=
12
AB=2，G为线段AB的中点，将△ADG沿GD折起，使平面ADG⊥平面BCDG，得到几何体A-BCDG．
（1）若E，F分别为线段AC，AD的中点，求证：EF∥平面ABG；
（2）求证：AG⊥平面BCDG；
（3）求VC-ABD的值
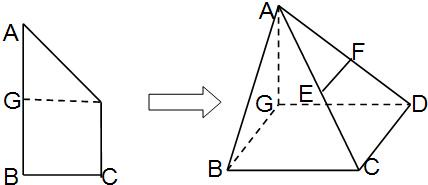
精英家教网
（2012•福建模拟）在直角梯形ABCD中，AD∥BC，AB=1，AD=
3
，AB⊥BC，CD⊥BD，如图1．把△ABD沿BD翻折，使得平面A′BD⊥平面BCD，如图2．

（Ⅰ）求证：CD⊥A′B；
（Ⅱ）求三棱锥A′-BDC的体积；
（Ⅲ）在线段BC上是否存在点N，使得A′N⊥BD？若存在，请求出
BN
BC
的值；若不存在，请说明理由．
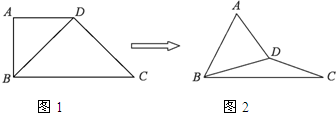
（2012•福建模拟）在直角梯形ABCD中，AD∥BC，BC=2AD=2AB=2
2
，∠ABC=90°，如图1．把△ABD沿BD翻折，使得平面ABD⊥平面BCD，如图2．
（Ⅰ）求证：CD⊥AB；
（Ⅱ）若点M为线段BC中点，求点M到平面ACD的距离；
（Ⅲ）在线段BC上是否存在点N，使得AN与平面ACD所成角为60°？若存在，求出
BN
BC
的值；若不存在，说明理由．
如图，在直角梯形ABCD中，AB∥CD，AB⊥AD，且AD=1，AB=2，CD=3，E、F分别为线段CD、AB上的点，且EF∥AD．将梯形沿EF折起，使得平面ADEF⊥平面BCEF，折后BD与平面ADEF所成角正切值为
2
2
．
（Ⅰ）求证：BC⊥平面BDE；
（Ⅱ）求平面BCEF与平面ABD所成二面角（锐角）的大小．
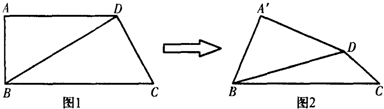（2013•许昌二模）在直角梯形ABCD中，AD∥BC，AB=1，AD=
3
，AB⊥BC，CD⊥BD，如图1，把△ABD沿BD翻折，使得平面A'BD⊥平面BCD，如图2．
（Ⅰ）求证：CD⊥A'B；
（Ⅱ）求三棱锥A'-BDC的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网