题目内容
f(x)为(-∞,+∞)上的减函数,a∈R,则( )A.f(a)<f(2a)
B.f(a2)<f(a)
C.f(a2+1)<f(a)
D.f(a2+a)<f(a)
【答案】分析:先比较题中变量的大小关系,再利用减函数中大自变量对应小函数值,小自变量对应大函数值来找答案即可.
解答:解:因为a∈R,所以a-2a=-a与0的大小关系不定,没法比较f(a)与f(2a)的大小,故A错
而a2-a=a(a-1)与0 的大小关系也不定,f(a2)与f(a)的大小,故B错;
又因为a2+1-a=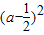 +
+ >0,
>0,
所以a2+1>a.又f(x)为(-∞,+∞)上的减函数,
故有f(a2+1)<f(a)故C对D错.
故选C.
点评:本题考查函数单调性的应用.当一个函数是减函数时,大自变量对应小函数值,小自变量对应大函数值.而当一个函数是增函数时,大自变量对应大函数值,小自变量对应小函数值.
解答:解:因为a∈R,所以a-2a=-a与0的大小关系不定,没法比较f(a)与f(2a)的大小,故A错
而a2-a=a(a-1)与0 的大小关系也不定,f(a2)与f(a)的大小,故B错;
又因为a2+1-a=
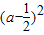 +
+ >0,
>0,所以a2+1>a.又f(x)为(-∞,+∞)上的减函数,
故有f(a2+1)<f(a)故C对D错.
故选C.
点评:本题考查函数单调性的应用.当一个函数是减函数时,大自变量对应小函数值,小自变量对应大函数值.而当一个函数是增函数时,大自变量对应大函数值,小自变量对应小函数值.

练习册系列答案
相关题目