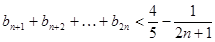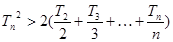题目内容
已知在数列![]() 中,
中,![]() ,
,![]() (
(![]() ÎR,
ÎR,![]() ÎR 且
ÎR 且![]() ¹0,
¹0,![]() N
N![]() ).
).
(1)若数列![]() 是等比数列,求
是等比数列,求![]() 与
与![]() 满足的条件;
满足的条件;
(2)当![]() ,
,![]() 时,一个质点在平面直角坐标系内运动,从坐标原点出发,第1次向右运动,第2次向上运动,第3次向左运动,第4次向下运动,以后依次按向右、向上、向左、向下的方向交替地运动,设第
时,一个质点在平面直角坐标系内运动,从坐标原点出发,第1次向右运动,第2次向上运动,第3次向左运动,第4次向下运动,以后依次按向右、向上、向左、向下的方向交替地运动,设第![]() 次运动的位移是
次运动的位移是![]() ,第
,第![]() 次运动后,质点到达点
次运动后,质点到达点![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
解析:(1)![]()
![]() ,
,![]() ,
,![]() ¹0,
¹0,
① 当![]() 时,
时,![]() ,显然
,显然![]() 是等比数列;
是等比数列;
② 当![]() 时,
时,![]() .
.
![]() 数列
数列![]() 是等比数列,
是等比数列,
∴![]() ,即
,即![]() ,化简得
,化简得![]() .
.
此时有![]() ,得
,得![]() ,
,
由 ![]() ,
,![]() ¹0, 得
¹0, 得![]() (
(![]() N
N![]() ),则数列
),则数列![]() 是等比数列.
是等比数列.
综上,![]() 与
与![]() 满足的条件为
满足的条件为![]() 或
或![]() (
(![]() ).
).
(2)当![]() ,
,![]() 时,
时,
∵![]() ,
,
∴![]() ,
,
依题意得:![]() ,
,![]() ,…,
,…,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]()
![]()
![]()
![]() .
.
令![]() ①
①
![]()
![]() ②
②
①-②得![]()
![]()
![]() .
.
∴![]() .
.

练习册系列答案
相关题目
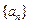 中,
中,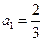
 ,
,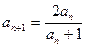 ,
,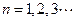
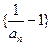 是
是 等比数列; (2)求数列
等比数列; (2)求数列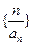 的前n项和。
的前n项和。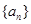 中,
中,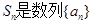 的前n项和,
的前n项和,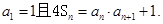
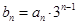 ,数列
,数列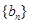 的前n项和为
的前n项和为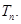 求
求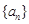 中,
中,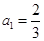 ,
,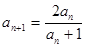 ,
,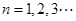
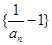 是等比数列; (2)求数列
是等比数列; (2)求数列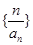 的前n项和。
的前n项和。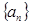 中,
中,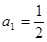 ,
,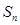 是其前
是其前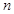 项和,且
项和,且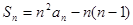 .
.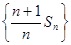 是等差数列;
是等差数列;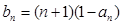 ,记数列
,记数列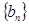 的前
的前 .
. 时,
时,