题目内容
14分)已知在数列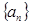 中,
中,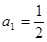 ,
,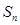 是其前
是其前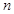 项和,且
项和,且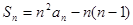 .
.
(1)证明:数列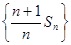 是等差数列;
是等差数列;
(2)令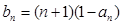 ,记数列
,记数列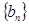 的前
的前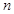 项和为
项和为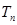 .
.
①;求证:当 时,
时,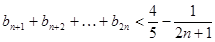
②: 求证:当 时,
时,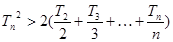
【答案】
解:由条件可得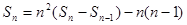 ,
,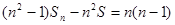
两边同除以 ,得:
,得: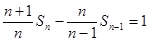
所以:数列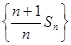 成等差数列,且首项和公差均为1………………4分
成等差数列,且首项和公差均为1………………4分
(2)由(1)可得: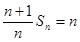 ,
,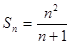 ,代入
,代入 可得
可得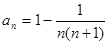 ,所以
,所以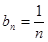 ,
,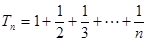 .………………………6分
.………………………6分
①当 时,
时,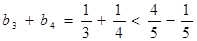 即
即 时命题成立
时命题成立
假设 时命题成立,即
时命题成立,即
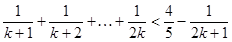
当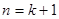 时,
时,
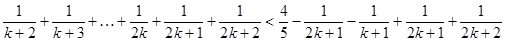
=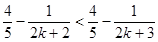 即
即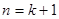 时命题也成立
时命题也成立
综上,对于任意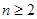 ,
,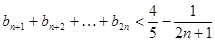 ………………………………9分
………………………………9分
②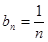 当
当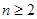 时,
时,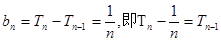
平方则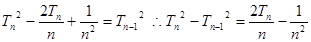
叠加得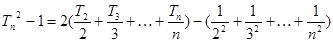

又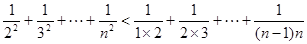
=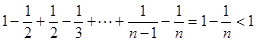

………………14分
【解析】略

练习册系列答案
相关题目
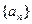 ,
,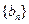 满足
满足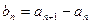 ,其中
,其中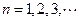 .
.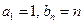 ,求数列
,求数列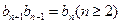 ,且
,且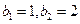 .
.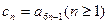 ,求证:数列
,求证:数列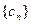 为等差数列;
为等差数列;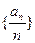 中任意一项的值均未在该数列中重复出现无数次. 求首项
中任意一项的值均未在该数列中重复出现无数次. 求首项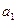 应满足的条件.
应满足的条件.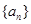 中,
中,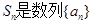 的前n项和,
的前n项和,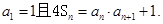
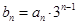 ,数列
,数列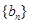 的前n项和为
的前n项和为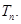 求
求 中,
中, ,且
,且 是
是 和
和 的等差中项.
的等差中项. 满足
满足 ,求
,求 项和
项和 .
.