Question

设椭圆

x2

a2

+

y2

b2

=1，a＞b＞0的左焦点为F₁，上顶点为A，过点A与AF₁垂直的直线分别交椭圆和x轴正半轴于P、Q两点，且P分向量

AQ

所成的比为λ．
（1）当λ∈（1，2）时，探求椭圆离心率（

1

e

-e）²的取值范围；
（2）当λ=

8

5

时，过A、Q、F₁三点的圆恰好与直线L：x+

3

y+3=0相切，求椭圆的方程．

Answer 1

分析：（1）根据P分向量

AQ

所成的比为λ，可得点P的坐标，代入椭圆方程，再利用

F1A

•

AQ

=0，联立可表示出（

1

e

-e）²，进而根据λ∈（1，2），可探求椭圆离心率（

1

e

-e）²的取值范围；
（2）当λ=

8

5

时，e-

1

e

=-

3

2

，故e=

1

2

，a=2c．利用圆恰好与直线L：x+

3

y+3=0相切，可求a=2，b=

3

，从而得到椭圆方程

解答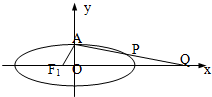：解：（1）设Q（x₀，0），F₁（-c，0），A（0，b），
∵P分向量

AQ

所成的比为λ，
∴P（

λx0

1+λ

，

b

1+λ

），∴（

λx0

1+λ

）²

1

a2

+（

b

1+λ

）²

1

b2

=1．        ①
而

F1A

=（c，b），

AQ

=（x₀，-b），

F1A

•

AQ

=0，
∴cx₀-b²=0．   ②
由①、②消去x₀，得（

λb2

1+λ

）²

1

c2a2

+（

1

1+λ

）²=1，
即λ²

b4

c2a2

=（1+λ）²-1，即（

1

e

-e）²=1+

2

λ

∈（2，3）．   
（2）当λ=

8

5

时，e-

1

e

=-

3

2

，
∴e=

1

2

，a=2c．
又∵△AF₁Q是直角三角形，其外接圆圆心是斜边中点，
∴圆心为（

b2 c +(-c)

2

，0）=（

a2-c2-c2

2c

，0）=（c，0），
半径为r=

b2 c +c

2

=

a2

2c

=a．
由圆恰好与直线L：x+

3

y+3=0相切，得

|c+3|

2

=a，
∴a=2，b=

3

．
∴椭圆方程为

x2

4

+

y2

3

=1．

点评：本题以椭圆为载体，考查椭圆的几何性质，考查直线与圆的位置关系，考查了椭圆的标准方程，有一定的综合性．