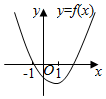题目内容
2.若直线x+y=1与曲线y=$\sqrt{a-{x}^{2}}$(a>0)恰有一个公共点,则a的取值范围是a=$\frac{1}{2}$或a>1.分析 将曲线y=$\sqrt{a-{x}^{2}}$(a>0)看成一个半圆,画出直线x+y=1与半圆恰有一个公共点时的情况,求解a的取值范围即可.
解答 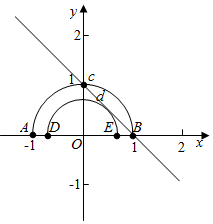 解:由曲线y=$\sqrt{a-{x}^{2}}$(a>0),知y≥0,
解:由曲线y=$\sqrt{a-{x}^{2}}$(a>0),知y≥0,
等式两边同时平方,整理可得x2+y2=a2,
即曲线y=$\sqrt{a-{x}^{2}}$(a>0)是以(0,0)点为圆心,以$\sqrt{a}$为半径的半圆(y≥0)
已知直线x+y=1,可在直角坐标系中给出图象(如下图)
由图象可知,当半圆的半径$\sqrt{a}$>1即a>1时或者半圆与直线相切时恰有一个公共交点,
当半圆与直线相切时,圆心(0,0)到直线的距离即为半圆的半径,此时$\sqrt{a}=\frac{|0×1+0×1-1|}{\sqrt{{1}^{2}+{1}^{2}}}=\frac{\sqrt{2}}{2}$,即a=$\frac{1}{2}$
所以当直线x+y=1与曲线y=$\sqrt{a-{x}^{2}}$(a>0)恰有一个公共点时,a的取值范围是a=$\frac{1}{2}$或a>1.
故答案为:a=$\frac{1}{2}$或a>1.
点评 对于直线和圆的交点个数问题,采用数形结合的思想来考虑较为直观、简单.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
12.在不等式组$\left\{\begin{array}{l}0≤x≤2\\ 0≤y≤2\end{array}\right.$表示的平面区域内任取一个点P(x,y),使得x+y≤1的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{12}$ |
13.若函数y=x+$\frac{1}{2x}+t$(x>0)有两个零点,则实数t的取值范围是( )
| A. | ($\sqrt{2}$,+∞) | B. | (2,+∞) | C. | (-∞,2) | D. | (-∞,-$\sqrt{2}$) |
7.程序框图如图所示,该程序运行后输出的S的值是( )


| A. | 2 | B. | -$\frac{1}{2}$ | C. | -3 | D. | $\frac{1}{3}$ |
14.已知平面向量$\overrightarrow{a}$=(2,0),$\overrightarrow{b}$=(-4,0),则向量$\overrightarrow{b}$在向量$\overrightarrow{a}$方向上的投影为( )
| A. | 4 | B. | -4 | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |
11.设z=$\frac{2i}{1+i}$(i是虚数单位),则z的模是( )
| A. | i | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{5}$ |
12.编辑一个计算机自动执行程序:1Φ1=2,mΦn=k,(m+1)Φn=k-1,mΦ(n+1)=k+2,则2011Φ2011的输出结果为( )
| A. | 2009 | B. | 2010 | C. | 2011 | D. | 2012 |