题目内容
9. 如图,已知直线与抛物线y2=2px(p>0)相交于A,B两点,且OA⊥OB,OD⊥AB交AB于D,且点D的坐标为(3,$\sqrt{3}$).
如图,已知直线与抛物线y2=2px(p>0)相交于A,B两点,且OA⊥OB,OD⊥AB交AB于D,且点D的坐标为(3,$\sqrt{3}$).(1)求p的值;
(2)若F为抛物线的焦点,M为抛物线上任意一点,求|MD|+|MF|的最小值.
分析 (1)设A(x1,y1),B(x2,y2),由AB⊥OD,kOD=$\frac{\sqrt{3}}{3}$.可得直线AB的斜率k=-$\sqrt{3}$.得到直线AB的方程为$y-\sqrt{3}=-\sqrt{3}(x-3)$,与抛物线方程联立化为3x2-(24+2p)x+48=0,利用根与系数的关系及其$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2=0,解得p.
(2)过点M作直线的垂线MN,垂足为N,则|MF|=|MN|,则当N,M,D三点共线时,|MD|+|MF|取得最小值.
解答 解:(1)设A(x1,y1),B(x2,y2),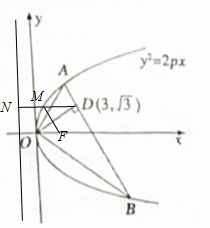
∵AB⊥OD,kOD=$\frac{\sqrt{3}}{3}$.
∴直线AB的斜率k=-$\sqrt{3}$.
∴直线AB的方程为$y-\sqrt{3}=-\sqrt{3}(x-3)$,化为$y=-\sqrt{3}x+4\sqrt{3}$.
联立$\left\{\begin{array}{l}{y=-\sqrt{3}x+4\sqrt{3}}\\{{y}^{2}=2px}\end{array}\right.$,化为3x2-(24+2p)x+48=0,
∴x1x2=16,x1+x2=$\frac{24+2p}{3}$.
∴y1y2=$(-\sqrt{3}{x}_{1}+4\sqrt{3})(-\sqrt{3}{x}_{2}+4\sqrt{3})$=3[x1x2-4(x1+x2)+16],
∵OA⊥OB,
∴$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2=4x1x2-12(x1+x2)+48=0,
∴64-12×$\frac{24+2p}{3}$+48=0,
解得p=2.
(2)过点M作直线的垂线MN,垂足为N,则|MF|=|MN|,
∴当N,M,D三点共线时,|MD|+|MF|取得最小值,为$3+\frac{p}{2}$=4.
点评 本题查克拉抛物线的定义标准方程及其性质、直线与抛物线相交问题转化为方程联立可得根与系数的关系、向量垂直与数量积的关系,考查了推理能力与计算能力,属于中档题.

最大值为( )
| A. | 2 | B. | $\sqrt{2}$+1 | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$+2 |
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 加工时间y(min) | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
(2)求回归方程;
(3)关于加工零件的个数与加工时间,你能得出什么结论?
 某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为$\frac{80π}{3}$立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>5)千元.设该容器的建造费用为y千元.
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为$\frac{80π}{3}$立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>5)千元.设该容器的建造费用为y千元.