题目内容
已知圆 ,圆
,圆 与圆
与圆 关于直线
关于直线 对称,则圆
对称,则圆 的方程为( )
的方程为( )
A. | B. |
C. | D. |
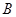
解析试题分析: 的圆心为
的圆心为 ,所以它关于直线
,所以它关于直线 对称的点为
对称的点为 ,对称后半径不变,所以圆
,对称后半径不变,所以圆 的方程为
的方程为 .
.
考点:直线及圆的方程.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
点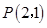 为圆
为圆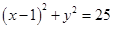 的弦
的弦 的中点,则直线
的中点,则直线 的方程为( )
的方程为( )
A. | B.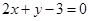 | C.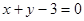 | D.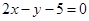 |
圆 的半径为 ( )
的半径为 ( )
A. | B. | C. | D. |
圆C的圆心在y轴正半轴上,且与x轴相切,被双曲线 的渐近线截得的弦长为
的渐近线截得的弦长为 ,则圆C的方程为( )
,则圆C的方程为( )
| A.x2+(y-1)2=1 | B.x2+(y- )2=3 )2=3 |
C.x2+(y- )2= )2= | D.x2+(y-2)2=4 |
设A,B为直线 与圆
与圆 的两个交点,则|AB|=( )
的两个交点,则|AB|=( )
| A.1 | B. | C. | D.2 |
已知点P(a,b)(ab≠0)是圆x2+y2=r2内的一点,直线m是以P为中点的弦所在的直线,直线l的方程为ax+by=r2,那么( )
| A.m∥l,且l与圆相交 | B.m⊥l,且l与圆相切 |
| C.m∥l,且l与圆相离 | D.m⊥l,且l与圆相离 |
已知M(x0,y0)为圆x2+y2=a2(a>0)内异于圆心的一点,则直线x0x+y0y=a2与该圆的位置关系是( )
| A.相切 | B.相交 | C.相离 | D.相切或相交 |
当a为任意实数时,直线(a-1)x-y+a+1=0恒过定点C,则以C为圆心,半径为 的圆的方程为( ).
的圆的方程为( ).
| A.x2+y2-2x+4y=0 |
| B.x2+y2+2x+4y=0 |
| C.x2+y2+2x-4y=0 |
| D.x2+y2-2x-4y=0 |
