题目内容

设动直线l垂直于x轴，与椭圆=1交于A、B两点，P是l上满足|PA||PB|=1的点，求P点的轨迹方程.

思路分析：由椭圆的方程可设A、B两点的坐标，代入|PA||PB|=1，可得一参数方程，消参即可得到所求P点的轨迹方程.

解：设P(x0,y0),A(2cosθ,sinθ),B(2cosθ,sinθ)x0=2cosθ,①

由|PA||PB|=1,得y02=2-2cos2θ±1,②

由①②消去参数,得y02=2-x02±1(|x0|≤2).

练习册系列答案
相关题目
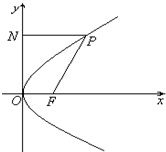精英家教网如图所示，点F(
p
2
，0)(p＞0)，点P为抛物线C：y2=2px上的动点，P到y轴的距离PN满足：|PF|=|PN|+
1
2
，直线l过点F，与抛物线交于A，B两点．
（1）求抛物线C的方程；
（2）设点Q（a，0）（a＜0），若直线l垂直于x轴，且向量
QA
和
QB
的夹角为
π
3
，求a的值；
（3）设M为线段AB的中点，求点M到直线y=x+1距离的最小值．
设动直线l垂直于x轴，且与椭圆x2+2y2=4交于A，B两点，P是l上满足
PA
•
PB
=1的点，求点P的轨迹方程．
已知直线y=-2上有一个动点Q，过Q作直线l垂直于x轴，动点P在直线l上，且
OP
⊥
OQ
，记点P的轨迹为C1，
（1）求曲线C1的方程；
（2）设直线l与x轴交于点A，且
OB
=
PA
(
OB
≠0)，试判断直线PB与曲线C1的位置关系，并证明你的结论；
（3）已知圆C2：x2+（y-a）2=2，若C1、C2在交点处的切线相互垂直，求a的值．

设动直线l垂直于x轴，且与椭圆x2＋2y2＝4交于A、B两点，P是l上满足＝1的点，求点P的轨迹方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网