题目内容
设等差数列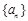 的前
的前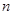 项和为
项和为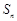 ,满足:
,满足: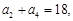
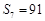 .递增的等比数列
.递增的等比数列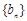 前
前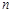 项和为
项和为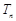 ,满足:
,满足: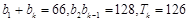 .
.
(Ⅰ)求数列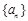 ,
,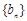 的通项公式;
的通项公式;
(Ⅱ)设数列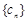 对
对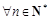 ,均有
,均有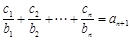 成立,求
成立,求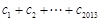 .
.
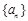 的前
的前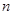 项和为
项和为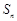 ,满足:
,满足: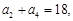
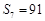 .递增的等比数列
.递增的等比数列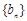 前
前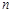 项和为
项和为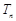 ,满足:
,满足: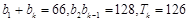 .
.(Ⅰ)求数列
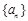 ,
,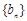 的通项公式;
的通项公式;(Ⅱ)设数列
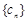 对
对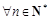 ,均有
,均有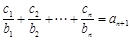 成立,求
成立,求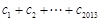 .
.(Ⅰ)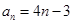 ,
,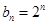 ; (Ⅱ)
; (Ⅱ)

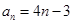 ,
,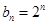 ; (Ⅱ)
; (Ⅱ)

试题分析:(Ⅰ)先由等差数列
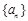 的性质得出
的性质得出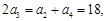 从而求出
从而求出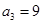 ,再结合
,再结合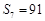 求出
求出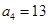 ,从而得出
,从而得出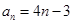 ;由
;由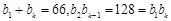 ,可构造方程
,可构造方程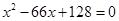 ,从而求出
,从而求出 ,由
,由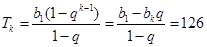 求出
求出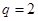 ,故
,故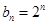 ;(Ⅱ)当
;(Ⅱ)当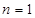 时,
时,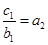 求得
求得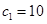 ;当
;当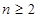 时由
时由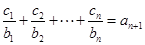 ,
,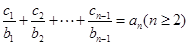 ,作差可得
,作差可得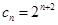 ,故
,故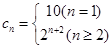 ,从而可求
,从而可求
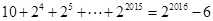 .
.试题解析:(Ⅰ)由题意
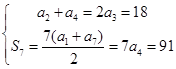 得
得 ,则
,则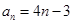 2分
2分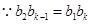 ,
,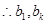 方程
方程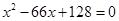 的两根,得
的两根,得 4分
4分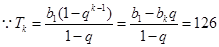 ,
, 代入求得
代入求得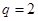 ,
, 6分
6分(Ⅱ)由
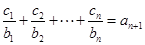 ,
,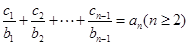
两式相减有

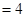
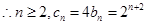 ,9分
,9分又
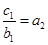 ,得
,得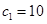
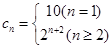
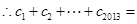
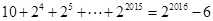
 项和
项和
练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
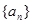 的前
的前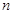 项的和为
项的和为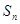 ,
, 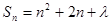 ,求证:数列
,求证:数列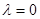 .
.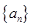 的首项为
的首项为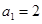 ,公比为
,公比为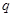 (
(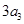 是
是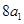 与
与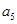 的等差中项;数列
的等差中项;数列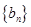 满足
满足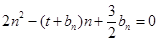 (
(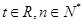 ).
).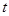 的值,使得数列
的值,使得数列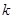 ,在
,在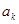 与
与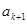 之间插入
之间插入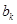 个2,得到一个新数列
个2,得到一个新数列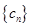 . 设
. 设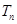 是数列
是数列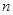 项和,试求满足
项和,试求满足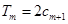 的所有正整数
的所有正整数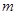 .
.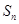 为等差数列
为等差数列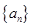 的前
的前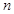 项和,且
项和,且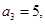
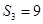 .
.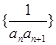 的前
的前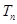 .
.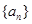 的公差为2,若
的公差为2,若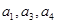 成等比数列,则a2=( )
成等比数列,则a2=( )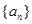 的前
的前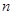 项和为
项和为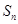 ,且
,且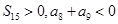 ,则使得
,则使得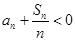 的最小的
的最小的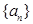 中,
中,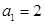 ,
,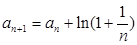 ,则
,则 =( )
=( )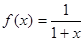 ,各项均为正数的数列
,各项均为正数的数列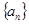 满足
满足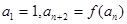 ,若
,若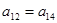 ,则
,则 .
.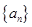 是等差数列,
是等差数列,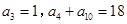 ,则首项
,则首项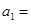 .
.