函数f(x)=x-1-2sinπx的所有零点之和等于5．题目和参考答案——青夏教育精英家教网——

题目内容

1．函数f（x）=x-1-2sinπx的所有零点之和等于5．

分析由f（x）=x-1-2sinπx=0得x-1=2sinπx，分别作出函数y=x-1和y=2sinπx的图象，利用对称性结合数形结合进行求解即可．

解答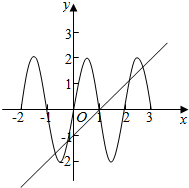解：由f（x）=x-1-2sinπx=0得x-1=2sinπx，
分别作出函数y=x-1和y=2sinπx的图象如图：
则两个函数都关于点（1，0）对称，
由图象知，两个函数共有5个交点，其中x=1是一个零点，
另外4个零点关于点（1，0）对称，
设对称的两个点的横坐标分别为x₁，x₂，
则x₁+x₂=2×1=2，
∴5个交点的横坐标之和为2+2+1=5．
故答案为：5．

点评本题主要考查函数交点个数以及数值的计算，根据函数图象的性质，利用数形结合是解决此类问题的关键，综合性较强．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

11．在直角坐标系xoy中，曲线C₁，C₂的参数方程分别为$\left\{\begin{array}{l}x=\sqrt{5}cosθ\\ y=\sqrt{5}sinθ\end{array}\right.$（θ为参数）和$\left\{\begin{array}{l}x=\sqrt{5}-\frac{{\sqrt{2}}}{2}t\\ y=-\frac{{\sqrt{2}}}{2}t\end{array}\right.$（t为参数）则曲线C₁，C₂的交点的极坐标（5，$\frac{3π}{2}$）或（5，0）．

12．已知数列{a_n}中a₁=1，关于x的方程x²-a_n+1•tan（cosx）+（2a_n+1）•tan1=0有唯一解，设b_n=na_n，数列{b_n}的前n项和为S_n，则S₉=（　　）

9．已知函数f（x）=e^x-ax一1（a∈R）．
（I）讨论函数y=f（x）的单调性并求其单调区间；
（Ⅱ）若函数F（x）=f（x）-x1nx在定义域内存在零点，试求实数a的取值范围；
（Ⅲ）若g（x）=1n（e^x-1）-lnx，且f[g（x）]＜f（x）在x∈（0，+∞）上恒成立，求实数a的取值范围．

16．设函数h（x）=x²-mx，g（x）=lnx．
（Ⅰ）设f（t）=m${∫}_{\frac{π}{2}}^{t}$（sinx+cosx）dx且f（2016π）=2，若函数h（x）与g（x）在x=x₀处的切线平行，求这两切线间的距离；
（Ⅱ）任意x＞0，不等式h（x）≥g（x）恒成立，求实数m的取值范围．

6．设函数f（x）=sin（ωx+φ）+cos（ωx+φ）（|φ|＜$\frac{π}{2}$）的图象可以由g（x）=2$\sqrt{2}$sinxcosx的图象向x轴负方向平移$\frac{π}{4}$个单位得到，则φ的值为（　　）

-$\frac{π}{8}$

13．已知点A（4，3），P是双曲线x²-y²=2右支上一点，F为双曲线的右焦点，则|PA|+|PF|的最小值是（　　）

$3\sqrt{5}-2\sqrt{2}$

$2\sqrt{5}+\sqrt{2}$

10．股票每天的涨、跌幅均不超过10%，即当涨了原价的10%后，便不能再涨，叫做涨停；当跌了原价的10%后，便不能再跌，叫做跌停．已知一支股票某天涨停，之后两天时间又跌回到原价，若这两天此股票股价的平均每天下跌的百分率为x，则x满足的方程是（　　）

1-2x=$\frac{9}{10}$

1-2x=$\frac{10}{11}$

（1-x）²=$\frac{9}{10}$

（1-x）²=$\frac{10}{11}$

11．已知函数f（x）=（mx+1）（1nx-3）．
（1）若m=1，求曲线y=f（x）在x=1处的切线方程；
（2）若函数f（x）在（0，+∞）上是增函数，求实数m的取值范围．