题目内容
已知函数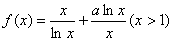 的图象经过
的图象经过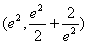
 其中e为自然对数的底数,e≈2.71
其中e为自然对数的底数,e≈2.71 ,
,
(Ⅰ)求实数a;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)证明:对于任意的n∈N*,都有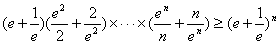 成立。
成立。
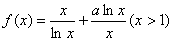 的图象经过
的图象经过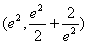
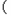 其中e为自然对数的底数,e≈2.71
其中e为自然对数的底数,e≈2.71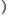 ,
,(Ⅰ)求实数a;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)证明:对于任意的n∈N*,都有
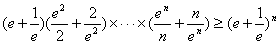 成立。
成立。解:(Ⅰ)由y=f(x)的图象过点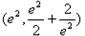 ,
,
得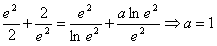 。
。
(Ⅱ)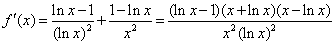 ,
,
由x>1知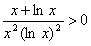 ,
,
令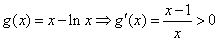 ,
,
故g(x)在(1,+∞)上为增函数,
当x>1时,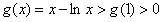 ,
,
令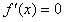 得x=e,
得x=e,
令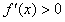 得,x>e;令
得,x>e;令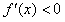 得
得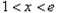 ,
,
故f(x)的增区间为(e,+∞),减区间为(1,e)。
(Ⅲ)由(Ⅱ)知,f(x)在区间(1,+∞)上的最小值为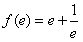 ,
,
即当x>1时,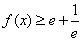 恒成立,
恒成立,
当n∈N*时,令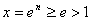 ,
,
则有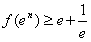 ,
,
即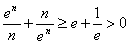 ,
,
故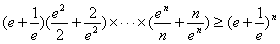 成立。
成立。
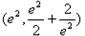 ,
,得
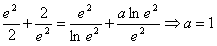 。
。 (Ⅱ)
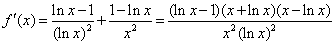 ,
,由x>1知
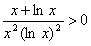 ,
,令
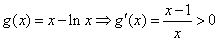 ,
,故g(x)在(1,+∞)上为增函数,
当x>1时,
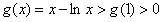 ,
,令
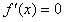 得x=e,
得x=e,令
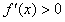 得,x>e;令
得,x>e;令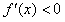 得
得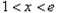 ,
,故f(x)的增区间为(e,+∞),减区间为(1,e)。
(Ⅲ)由(Ⅱ)知,f(x)在区间(1,+∞)上的最小值为
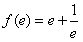 ,
,即当x>1时,
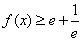 恒成立,
恒成立,当n∈N*时,令
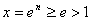 ,
,则有
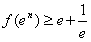 ,
,即
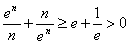 ,
,故
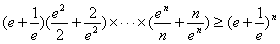 成立。
成立。 
练习册系列答案
相关题目












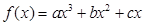 在点
在点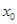 处取得极大值
处取得极大值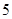 ,
,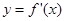 的图象经过点
的图象经过点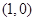 ,
,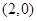 ,如图所示.
,如图所示.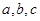 的值.
的值. 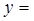

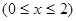 与
与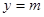 有两个不同的交点,
有两个不同的交点,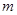 的取值范围。
的取值范围。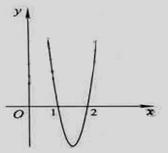
 的图象经过原点,其导函数为
的图象经过原点,其导函数为 ,数列
,数列 的前
的前 项和为
项和为 ,点
,点 均在函数
均在函数 的表达式;
的表达式;