题目内容
21.已知数列
、
与函数
、
，
满足条件：
，
.
（I）若
，
，
，且
存在，求t的取值范围，并求
（用
表示）；
（II）若函数
为
上的增函数，
，
，
，证明对任意的
，
.
（I）解法一：由题设知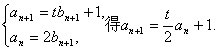又知t≠2,可得
由f(b)≠g(b),t≠2,t≠0,可知a1+=tb+0,所以是等比数列，其首项为tb+,公比为.于是
+=(tb+),即an=(tb+)-.
又liman存在，可得0＜||＜1,所以-2＜t＜2且t≠0.
解法二:由题设知tbn+1=2bn+1,且t≠2,可得
bn+1+
由f(b)≠g(b),t≠2,t≠0,可知b+所以是首项为b+公比为的等比例数.
bn+
,即bn=
由
,可知,若
存在,则
存在.于是可得0＜|
|＜1,所以-2＜t＜2且t≠0.
=
=
解法三：由题设知tbn+1=2bn+1,即
bn+1=
①
于是有
②
②-①得bn+2-bn+1=
,令cn=bn+1-bn,得cn+1=
由f(b)≠g(b),t≠2,t≠0可知c1=b2-b1=
是首项为b2-b1,公比为
的等比数列，于是
bn+1=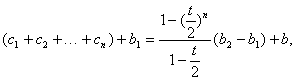
an=2bn+1=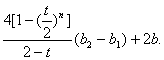
又
存在，可得0＜|
|＜1,所以-2＜t＜2且t
0.
=
说明:数列{an}通项公式的求法和结果的形式均不唯一,其他过程和结果参照以上评分标准.
（II）证明:因为g(x)=f--1(x),所以an=g(bn+1)=f -1 (bn+1),即bn+1=f(an).
下面用数学归纳法证明 an+1＜an(n
N*).
(1)当n=1时,由f(x)为增函数,且f(1)＜1,得
a1=f(b1)=f(1)＜1,
b2=f(a1)＜f(1)＜1,
a2=f(b2)＜f(1)=a1,
即a2＜a1,结论成立.
(2)假设n=k同结论成立,即ak+1＜ak .由f(x)为增函数，得f(ak+1)＜f(ak)，即bk+2＜bk+1 ，
进而得
f(bk+2)＜f(bk+1),即ak+2＜ak+1 .
这就是说当n=k+1时，结论也成立.
根据（1）和（2）可知，对任意的n∈N*，an+1＜an.
备战中考寒假系列答案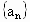
、
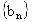与函数f(x)、g(x)，x
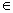R满足条件：
，
．
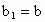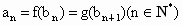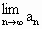存在，求t的取值范围，并求
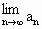(用t表示)；
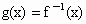，b=1，f(1)＜1，证明对任意的
，
．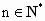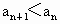