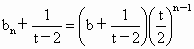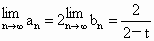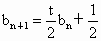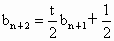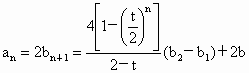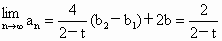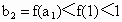题目内容
(2007
辽宁,21)已知数列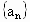 、
、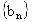 与函数f(x)、g(x),x
与函数f(x)、g(x),x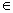 R满足条件:
R满足条件: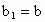 ,
,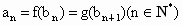 .
.
(1)
若f(x)=tx+1(t≠0,t≠2),g(x)=2x,f(b)≠g(b),且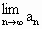 存在,求t的取值范围,并求
存在,求t的取值范围,并求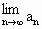 (用t表示);
(用t表示);
(2)
若函数y=f(x)为R上的增函数,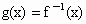 ,b=1,f(1)<1,证明对任意的
,b=1,f(1)<1,证明对任意的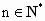 ,
,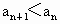 .
.
答案:略
解析:
提示:
解析:
|
解析: (1)解法一:由题设知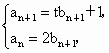 得 得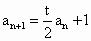 .又已知t≠2,可得 .又已知t≠2,可得 . .
由 f(b)≠g(b),t≠2,t≠0,可知 , ,
所以 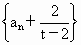 是等比数列,其首项为 是等比数列,其首项为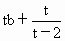 , ,
公比为 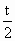 .于是 .于是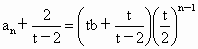 , ,
即 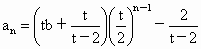 .又 .又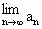 存在,可得 存在,可得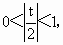
所以- 2<t<2且t≠0.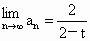 . .
解法二:由题设知 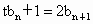 , ,
且 t≠2,可得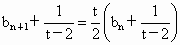 . .
由 f(b)≠g(b),t≠2,t≠0,可知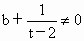 , ,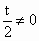 ,所以 ,所以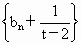 是首项为 是首项为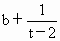 ,公比为 ,公比为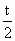 的等比数列. 的等比数列.
即 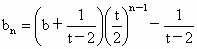 . .
由 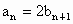 可知,若 可知,若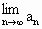 存在,则 存在,则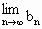 存在. 存在.
于是可得 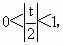 所以-2<t<2且t≠0. 所以-2<t<2且t≠0.
解法三:由题设知 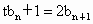 ,即 ,即
②-①得 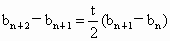 , ,
令 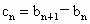 ,得 ,得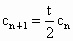 . .
由 f(b)≠g(b),t≠2,t≠0可得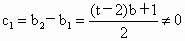 , ,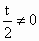 ,所以 ,所以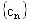 是首项为 是首项为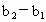 ,公比为 ,公比为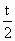 的等比数列. 的等比数列.
于是 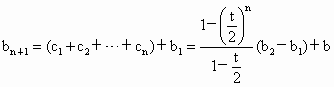 , ,
又 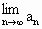 存在,可得 存在,可得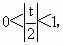
所以- 2<t<2且t≠0.
说明:数列 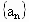 通项公式的求法和结果的表达形式均不唯一,其他过程和结果参照以上评分标准. 通项公式的求法和结果的表达形式均不唯一,其他过程和结果参照以上评分标准.
(2) 证明:因为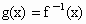 , ,
所以 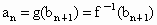 ,即 ,即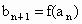 . .
下面用数学归纳法证明 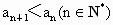 . .
①当 n=1时,由f(x)为增函数,且 f(1)<1,得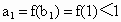 , ,
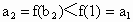 , ,
即 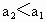 ,结论成立. ,结论成立.
②假设 n=k时结论成立,即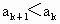 . .
由 f(x)为增函数,得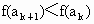 ,即 ,即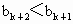 , ,
进而得 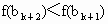 ,即 ,即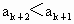 . .
这就是说当 n=k+1时,结论也成立.根据①和②可知,对任意的  , ,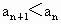 . . |
提示:
|
剖析:本题主要考查数列的定义、数列的递推公式、等比数列、函数、不等式等基础知识,考查运用数学归纳法解决问题的能力. |

练习册系列答案
相关题目