��Ŀ����
����Ŀ����ijУ�߶��꼶ѧ���μ����������������ͳ�ƣ������ȡM��ѧ����Ϊ�������õ���M��ѧ���μ���������Ĵ��������ݴ�����������Ƶ����Ƶ�ʵ�ͳ�Ʊ���Ƶ�ʷֲ�ֱ��ͼ���£�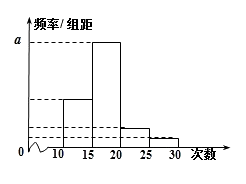

��1���������M��P��ͼ�� ![]() ��ֵ��
��ֵ��
��2������У�߶�ѧ����240�ˣ��Թ��Ƹ�У�߶�ѧ���μ���������Ĵ���������[10,15]�ڵ�������
��3������ȡ�����У��Ӳμ���������Ĵ���������20�ε�ѧ������ѡ2�ˣ�������һ�˲μ������������������[25,30]�ڵĸ��ʣ�
���𰸡�
��1���⣺�ɷ��� ![]() �ڵ�Ƶ����
�ڵ�Ƶ���� ![]() ��Ƶ����
��Ƶ���� ![]() ֪��
֪�� ![]() ������
������ ![]()
��ΪƵ��֮��Ϊ ![]() ������
������ ![]() ��
�� ![]() .
.![]()
��Ϊ ![]() �Ƕ�Ӧ����
�Ƕ�Ӧ���� ![]() ��Ƶ���������̣�����
��Ƶ���������̣����� ![]()
��2���⣺��Ϊ��У����ѧ����240�ˣ����� ![]() �ڵ�Ƶ����
�ڵ�Ƶ���� ![]() ��
��
���Թ��Ƹ�У����ѧ���μ���������Ĵ����ڴ������ڵ�����Ϊ60��
��3���⣺��������μ���������Ĵ���������20�ε�ѧ������ ![]() �ˣ�
�ˣ�
�������� ![]() �ڵ���Ϊ
�ڵ���Ϊ ![]() ��������
�������� ![]() �ڵ���Ϊ
�ڵ���Ϊ ![]() .
.
����ѡ ![]() �˹���
�˹��� ![]()
![]() ��
�� ![]() 15�������
15�������
�����˶��� ![]() ��ֻ����
��ֻ���� ![]() һ��
һ��
�����������Ϊ ![]() .��ԼΪ
.��ԼΪ ![]() ��
��
��������(1)����Ƶ�ʣ�Ƶ�������������Ĺ�ϵ��Ƶ�ʵ���Ƶ�����������������ٸ�����֪����ֵ�������M��p��a��ֵ��(2)��Ƶ�ʺ�Ƶ����ͳ�Ʊ���֪���߶�ѧ���вμ���������Ĵ���������[10,15]�ڵ�Ƶ��Ϊ0.25���ɴ��ܹ��Ƴ���У�߶�ѧ���μ���������Ĵ����������ڵ�����Ϊ60�ˡ�(3)��������������У��μ���������Ĵ���������20�ε�ѧ������6�ˣ���������оٳ������¼��������������¼����ɶ����¼��ĸ�����������

 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�