题目内容
【题目】如图，椭圆E： 
=1（a＞b＞0）经过点A（0，﹣1），且离心率为 
． （I）求椭圆E的方程；
（II）经过点（1，1），且斜率为k的直线与椭圆E交于不同两点P，Q（均异于点A），问直线AP与AQ的斜率之和是否为定值，若是，求出这个定值；若不是，请说明理由．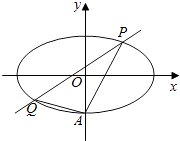
【答案】解：（Ⅰ）由题意知 
，b=1，结合a2=b2+c2 ， 解得 
， ∴椭圆的方程为 
；
（Ⅱ）由题设知，直线PQ的方程为y=k（x﹣1）+1 （k≠2），代入 ，得
（1+2k2）x2﹣4k（k﹣1）x+2k（k﹣2）=0，
由已知△＞0，设P（x1 ， y1），Q（x2 ， y2），x1x2≠0，
则 
， 
，
从而直线AP与AQ的斜率之和：
= 
= 
【解析】（Ⅰ）由题意可得b=1，结合椭圆的离心率及隐含条件求得a，则椭圆E的方程可求；（Ⅱ）设出直线PQ的方程，联立直线方程和椭圆方程，然后借助于根与系数的关系整体运算得答案．
练习册系列答案
相关题目
