题目内容
已知AB,CD分别为椭圆的长轴和短轴,若
=
,且
•
=0,则椭圆的离心率是
.
| AQ |
| 1 |
| 2 |
| AD |
| AD |
| CQ |
2
|
2
|
分析:利用向量的中点坐标公式可得点Q的坐标,再利用数量积运算
•
=0,即可得到a,b的关系式,利用离心率计算公式即可得出.
| AD |
| CQ |
解答:解:设椭圆的标准方程为
+
=1(a>b>0).
则A(-a,0),B(a,0),C(-b,0),D(0,b),
∵
=
,∴Q(-
,
).
∴
=(a,b),
=(-
+b,
).
∵
•
=0,∴a(-
+b)+
=0,化为(
)2+2•
-1=0,
解得
=
-1.
∴e=
=
=
.
故答案为
.
| x2 |
| a2 |
| y2 |
| b2 |
则A(-a,0),B(a,0),C(-b,0),D(0,b),
∵
| AQ |
| 1 |
| 2 |
| AD |
| a |
| 2 |
| b |
| 2 |
∴
| AD |
| CQ |
| a |
| 2 |
| b |
| 2 |
∵
| AD |
| CQ |
| a |
| 2 |
| b2 |
| 2 |
| b |
| a |
| b |
| a |
解得
| b |
| a |
| 2 |
∴e=
| c |
| a |
1-(
|
2
|
故答案为
2
|
点评:熟练掌握向量的中点坐标公式、数量积运算、离心率计算公式是解题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
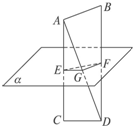 已知AB、CD为异面线段,E、F分别为AC、BD中点,过E、F作 平面α∥AB.
已知AB、CD为异面线段,E、F分别为AC、BD中点,过E、F作 平面α∥AB. =
=
 ,且
,且 ,则椭圆的离心率是 .
,则椭圆的离心率是 . =
=
 ,且
,且 ,则椭圆的离心率是 .
,则椭圆的离心率是 .