Question

8．若P满足$\frac{{x}^{2}}{4}$+y²=1（y≥0），则$\frac{y-2}{x-4}$的最小值是$\frac{4-\sqrt{7}}{6}$．

Answer 1

分析 通过记Q（4，2）可知k=$\frac{y-2}{x-4}$即为过椭圆上点P与点Q的直线的斜率，通过联立直线PQ与椭圆方程并令△=0，进而计算即得结论．

解答 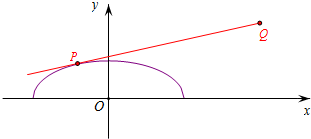解：记Q（4，2），k=$\frac{y-2}{x-4}$，则所求值k即为过椭圆上点P与点Q的直线的斜率，
易知直线PQ的方程为：y=kx+2-4k，并与椭圆方程联立，
消去x整理得：（4k²+1）x²-16k（2k-1）x+16（2k-1）²-4=0，
要使k最小，只需上述方程只有唯一一个解，
即△=[-16k（2k-1）]²-4（4k²+1）[16（2k-1）²-4]=0，
化简得：12k²-16k+3=0，
解得：k=$\frac{4+\sqrt{7}}{6}$（舍）或k=$\frac{4-\sqrt{7}}{6}$，
故答案为：$\frac{4-\sqrt{7}}{6}$．

点评 本题考查椭圆的简单性质，考查数形结合能力，注意解题方法的积累，属于中档题．