题目内容
13．已知函数f（x）=$\frac{{{x^2}-4x+5}}{x-2}$（x＞2），当且仅当x=3时，f（x）取到最小值为2．分析 变形利用基本不等式的性质即可得出．
解答 解：∵x＞2，∴x-2＞0，
∴函数f（x）=$\frac{{{x^2}-4x+5}}{x-2}$=$\frac{（x-2）^{2}+1}{x-2}$
=（x-2）+$\frac{1}{x-2}$≥2$\sqrt{（x-2）•\frac{1}{x-2}}$=2，当且仅当x=3时取等号，
故最小值为2，
故答案为：3，2．
点评 本题考查了基本不等式的性质，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
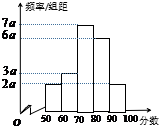在一次数学测试中，某班40名学生的成绩频率分布直方图如图所示（学生成绩都在[50，100]之间）．