题目内容
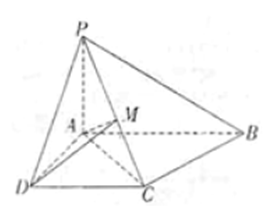
如图,在四面体ABCD中,CB=CD,AD⊥BD,点E,F分别是AB,BD的中点.
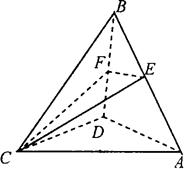
(Ⅰ)求证:平面EFC⊥平面BCD;
(Ⅱ)若平面ABD⊥平面BCD,且AD=BD=BC=1,
求三棱锥B-ADC的体积.

(Ⅰ)求证:平面EFC⊥平面BCD;
(Ⅱ)若平面ABD⊥平面BCD,且AD=BD=BC=1,
求三棱锥B-ADC的体积.
(Ⅰ)见解析 (Ⅱ) .
.
 .
.(1)根据面面垂直的判定定理,只须证明一个平面经过另一个平面的垂线,本小题证明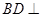 面
面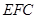 .即可。
.即可。
(2)利用三棱锥可换度的特性,本小题可以转化为求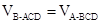
(Ⅰ)∵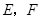 分别是
分别是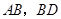 的中点, ∴
的中点, ∴ 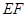 ∥
∥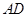 .……………1分
.……………1分
又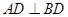 ,∴
,∴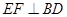 . ∵
. ∵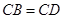 ,∴
,∴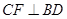 .……3分
.……3分
∵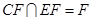 ,∴
,∴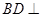 面
面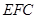 ∵
∵ 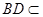 面
面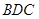 ,∴平面
,∴平面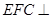 平面
平面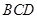 .
.
(Ⅱ) ∵ 面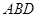
 面
面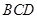 ,且
,且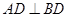 , ∴
, ∴ 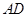
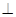 面
面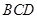 .………8分
.………8分
由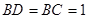 和
和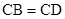 ,得
,得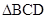 是正三角形. ………10分
是正三角形. ………10分
所以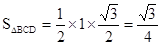 , ∴
, ∴ 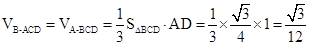
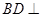 面
面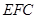 .即可。
.即可。(2)利用三棱锥可换度的特性,本小题可以转化为求
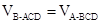
(Ⅰ)∵
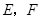 分别是
分别是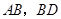 的中点, ∴
的中点, ∴ 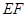 ∥
∥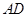 .……………1分
.……………1分又
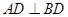 ,∴
,∴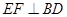 . ∵
. ∵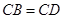 ,∴
,∴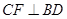 .……3分
.……3分∵
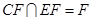 ,∴
,∴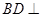 面
面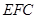 ∵
∵ 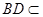 面
面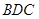 ,∴平面
,∴平面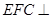 平面
平面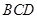 .
. (Ⅱ) ∵ 面
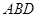
 面
面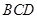 ,且
,且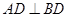 , ∴
, ∴ 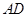
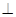 面
面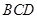 .………8分
.………8分由
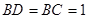 和
和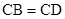 ,得
,得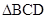 是正三角形. ………10分
是正三角形. ………10分所以
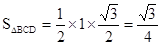 , ∴
, ∴ 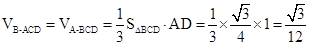

练习册系列答案
相关题目
 中,
中,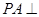 平面
平面 四边形
四边形 为正方形,
为正方形, 点在
点在 上的射影为
上的射影为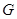 点.
点.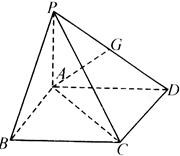
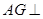 平面
平面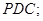
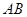 上是否存在一点
上是否存在一点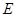 ,使得
,使得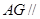 平面
平面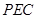 .若存在,求出
.若存在,求出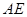 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
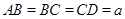 ,
,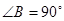 ,
,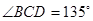 ,沿对角线
,沿对角线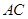 将
将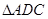 折起,使面
折起,使面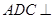 面
面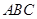 ,
,
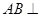 面
面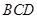 ;
;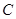 到面
到面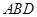 的距离.
的距离.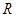 的球内部装4个有相同半径
的球内部装4个有相同半径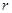 的小球,则小球半径
的小球,则小球半径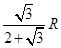
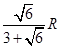
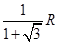
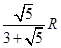
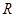 ,若甲地位于北纬
,若甲地位于北纬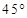 东经
东经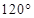 ,乙地位于南纬
,乙地位于南纬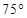 东经
东经



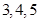 ,则这个长方体的对角线长为__________
,则这个长方体的对角线长为__________