题目内容
11．已知函数y=f（x）的图象在点M（1，f（1））处的切线方程是y=$\frac{1}{2}$x+2，则f（1）+f′（1）=3．分析 因为切点坐标一定满足切线方程，所以据此可以求出f（1）的值，又因为切线的斜率是函数在切点处的导数，就可求出f′（1）的值，把f（1）和f′（1）代入即可．
解答 解：∵点M（1，f（1））是切点，
∴点M在切线上，
∴f（1）=$\frac{1}{2}$+2=$\frac{5}{2}$，
∵函数y=f（x）的图象在点M（1，f（1））处的切线的方程是y=$\frac{1}{2}$x+2，
∴切线斜率是$\frac{1}{2}$，
即f′（1）=$\frac{1}{2}$，
∴f（1）+f'（1）=$\frac{5}{2}$+$\frac{1}{2}$=3．
故答案为：3．
点评 本题主要考查函数的切线斜率与导数的关系，属于导数的几何意义的应用，属于基础题．
练习册系列答案
智慧小复习系列答案
相关题目
1．用“五点法”作函数y=-sinx，x∈[0，2π]的简图．
（1）列表
（2）描点作图．
（1）列表
| x | ||||||
| sinx | ||||||
| -sinx |
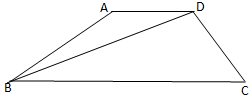在四边形ABCD中，AD∥BC，AB=$\sqrt{3}$，AD=1，A=$\frac{5π}{6}$