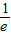题目内容
函数y=lnx在x=
处的切线与坐标轴所围图形的面积是( )
| 1 |
| e |
A.
| B.
| C.
| D.2e |
由题意得,y′=
,切点坐标(
,-1),
把x=
代入得,在x=
处的切线的斜率是e,
则在x=
处的切线方程是:y+1=e(x-
),
即ex-y-2=0,则y=ex-2,
令x=0,得y=-2;令y=0,x=
,
∴在x=
处切线与坐标轴所围图形的面积是:
s=
×2×
=
,
故选B.
| 1 |
| x |
| 1 |
| e |
把x=
| 1 |
| e |
| 1 |
| e |
则在x=
| 1 |
| e |
| 1 |
| e |
即ex-y-2=0,则y=ex-2,
令x=0,得y=-2;令y=0,x=
| 2 |
| e |
∴在x=
| 1 |
| e |
s=
| 1 |
| 2 |
| 2 |
| e |
| 2 |
| e |
故选B.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 处的切线与坐标轴所围图形的面积是( )
处的切线与坐标轴所围图形的面积是( )