题目内容
已知矩阵M= ,向量α=
,向量α= ,β=
,β= .
.
(1)求向量3α+ β在TM作用下的象;
β在TM作用下的象;
(2)求向量4Mα-5Mβ.
 ,向量α=
,向量α= ,β=
,β= .
.(1)求向量3α+
 β在TM作用下的象;
β在TM作用下的象;(2)求向量4Mα-5Mβ.
(1) (2)
(2)
 (2)
(2)
(1)因为3α+ β=3
β=3 +
+
 =
= +
+ =
= ,所以M
,所以M =
=
 =
= .(2)4Mα-5Mβ=M(4α-5β)=
.(2)4Mα-5Mβ=M(4α-5β)=
 =
= .
.
 β=3
β=3 +
+
 =
= +
+ =
= ,所以M
,所以M =
=
 =
= .(2)4Mα-5Mβ=M(4α-5β)=
.(2)4Mα-5Mβ=M(4α-5β)=
 =
= .
.
练习册系列答案
相关题目
 =1在(x,y)→(x′,y′)=(x+2y,y)对应的变换下变换成另一个图形F′,试求F′的解析式.
=1在(x,y)→(x′,y′)=(x+2y,y)对应的变换下变换成另一个图形F′,试求F′的解析式.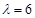 ,其对应的一个特征向量e=
,其对应的一个特征向量e=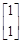 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点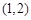 变换成点
变换成点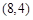 .
. ,向量
,向量 。
。 的特征值和特征向量;
的特征值和特征向量; .
. 有特征向量
有特征向量 =
= ,
, =
= ,相应的特征值为λ1,λ2.
,相应的特征值为λ1,λ2. =
= ,求M100
,求M100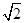 ),求△OAB在矩阵MN的作用下变换所得到的图形的面积,其中矩阵M=
),求△OAB在矩阵MN的作用下变换所得到的图形的面积,其中矩阵M=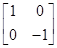 ,N=
,N=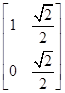 .
.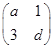 有特征值λ=-1及对应的一个特征向量e1=
有特征值λ=-1及对应的一个特征向量e1=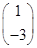 .
. 的特征多项式.
的特征多项式.