题目内容
直四棱柱ABCD-A1B1C1D1中,底面是边长为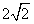 的正方形,侧棱长为4。
的正方形,侧棱长为4。
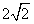 的正方形,侧棱长为4。
的正方形,侧棱长为4。 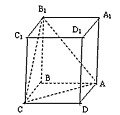
(1)求证:平面B1AC⊥平面BDD1B1;
(2)求点D1到平面B1AC的距离d;
(3)求三棱锥B1-ACD1的体积V。
(2)求点D1到平面B1AC的距离d;
(3)求三棱锥B1-ACD1的体积V。
解:(1)证明“略”;
(2) ;
;
(3) 。
。
(2)
 ;
;(3)
 。
。
练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
题目内容
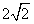 的正方形,侧棱长为4。
的正方形,侧棱长为4。 
 ;
; 。
。
 初中暑期衔接系列答案
初中暑期衔接系列答案