题目内容
直线 与双曲线
与双曲线 仅有一个公共点,则实数
仅有一个公共点,则实数 的值为
的值为
| A.1 | B.-1 | C.1或-1 | D.1或-1或0 |
C
解析试题分析:由 得:
得: ,
,
当 ,此时方程
,此时方程 只有一根,所以直线与双曲线仅有一个公共点;
只有一根,所以直线与双曲线仅有一个公共点;
当 时,要满足题意需
时,要满足题意需 ,此时无解。
,此时无解。
所以直线 与双曲线
与双曲线 仅有一个公共点,则实数
仅有一个公共点,则实数 的值为1或-1。
的值为1或-1。
考点:直线与双曲线的位置关系。
点评:在判断直线与双曲线的位置关系时,一般的方法是联立,组成方程组,消元,判断方程解的个数。一定要注意讨论二次项系数是否为0的情况。

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知抛物线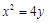 的焦点
的焦点 和点
和点 为抛物线上一点,则
为抛物线上一点,则 的最小值是( )
的最小值是( )
| A.3 | B.9 | C.12 | D.6 |
椭圆 的焦点坐标是( )
的焦点坐标是( )
A.(0, )、(0, )、(0, ) ) | B. (0,-1)、(0,1) |
| C.(-1,0)、(1,0) | D.( ,0)、( ,0)、( ,0) ,0) |
若抛物线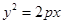 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )
| A.-2 | B.2 | C.-4 | D.4 |
一动圆圆心在抛物线 上,且动圆恒与直线
上,且动圆恒与直线 相切,则动圆必过定点
相切,则动圆必过定点
A.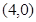 | B. | C. | D. |
过椭圆 的右焦点F2作倾斜角为
的右焦点F2作倾斜角为 弦AB,则|AB︳为( )
弦AB,则|AB︳为( )
A. | B. | C. | D. |
直线 与曲线
与曲线 相切于点
相切于点 ,则
,则 的值为 ( )
的值为 ( )
| A.-3 | B.9 |
| C.-15 | D.-7 |
 的左焦点作直线交椭圆于
的左焦点作直线交椭圆于 、
、 两点,若存在直线使坐标原点
两点,若存在直线使坐标原点 恰好在以
恰好在以 为直径的圆上,则椭圆的离心率取值范围是
为直径的圆上,则椭圆的离心率取值范围是
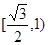


 +
+ =1的两焦点,经点F2的直线交椭圆于点A、B,若|AB|=5,则|AF1|+|BF1|等于( )
=1的两焦点,经点F2的直线交椭圆于点A、B,若|AB|=5,则|AF1|+|BF1|等于( )