题目内容
以双曲线
-
=1的焦点为顶点，顶点为焦点的椭圆方程是 ．
【答案】分析：先求出双曲线的顶点和焦点，从而得到椭圆的焦点和顶点，进而得到椭圆方程．
解答：解：双曲线
的顶点为（2，0）和（-2，0），焦点为（-4，0）和（4，0）．
∴椭圆的焦点坐标是（2，0）和（-2，0），顶点为（-4，0）和（4，0）．
∴椭圆方程为
+
=1．
故答案为：
+
=1．
点评：本题考查双曲线和椭圆的性质和应用，解题时要注意区分双曲线和椭圆的基本性质．
解答：解：双曲线
的顶点为（2，0）和（-2，0），焦点为（-4，0）和（4，0）．∴椭圆的焦点坐标是（2，0）和（-2，0），顶点为（-4，0）和（4，0）．
∴椭圆方程为
+=1．故答案为：
+=1．点评：本题考查双曲线和椭圆的性质和应用，解题时要注意区分双曲线和椭圆的基本性质．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
=1的焦点为焦点，离心率e=2的双曲线方程是( )
=1 B.
=1
=1 D.
=1
+
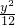=1的焦点为顶点,顶点为焦点的双曲线方程是________________.
-
=1的焦点为顶点，顶点为焦点的椭圆方程是________．
-
=1的焦点为顶点，顶点为焦点的椭圆方程是 ．