题目内容
设函数![]() .
.
(Ⅰ)当a=1时,求曲线f(x)在x=1处的切线方程;
(Ⅱ)当![]() 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(Ⅲ)在(Ⅱ)的条件下,设函数![]() ,若对于∀x1∈[1,2],∃x2∈[0,1],使f(x1)≥g(x2)成立,求实数b的取值范围.
,若对于∀x1∈[1,2],∃x2∈[0,1],使f(x1)≥g(x2)成立,求实数b的取值范围.
解答:
解:函数f(x)的定义域为(0,+∞),![]() (2分)
(2分)
(Ⅰ)当a=1时,f(x)=lnx﹣x﹣1,∴f(1)=﹣2,![]() ,
,
∴f'(1)=0,∴f(x)在x=1处的切线方程为y=﹣2(5分)
(Ⅱ)![]() =
=![]() (6分)
(6分)
令f'(x)<0,可得0<x<1,或x>2;令f'(x)>0,可得1<x<2
故当![]() 时,函数f(x)的单调递增区间为(1,2);单调递减区间为(0,1),(2,+∞).(8分)
时,函数f(x)的单调递增区间为(1,2);单调递减区间为(0,1),(2,+∞).(8分)
(Ⅲ)当![]() 时,由(Ⅱ)可知函数f(x)在(1,2)上为增函数,
时,由(Ⅱ)可知函数f(x)在(1,2)上为增函数,
∴函数f(x)在[1,2]上的最小值为f(1)=![]() (9分)
(9分)
若对于∀x1∈[1,2],∃x2∈[0,1]使f(x1)≥g(x2)成立,等价于g(x)在[0,1]上的最小值不大于f(x)在(0,e]上的最小值![]() (*) (10分)
(*) (10分)
又![]() ,x∈[0,1]
,x∈[0,1]
①当b<0时,g(x)在[0,1]上为增函数,![]() 与(*)矛盾
与(*)矛盾
②当0≤b≤1时,![]() ,由
,由![]() 及0≤b≤1得,
及0≤b≤1得,![]()
③当b>1时,g(x)在[0,1]上为减函数,![]() ,
,
此时b>1(11分)
综上,b的取值范围是![]() (12分)
(12分)

练习册系列答案
相关题目
 。
。 的极值;
的极值; 2时,讨论函数
2时,讨论函数 成立,求
成立,求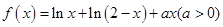 。
。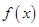 的单调区间。
的单调区间。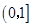 上的最大值为
上的最大值为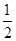 ,求a的值。
,求a的值。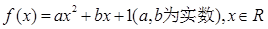 ,设函数
,设函数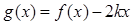 ,
,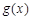 在
在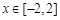 上的最小值
上的最小值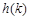 .
.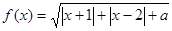 。
。 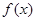 的定义域。
的定义域。