题目内容
（本小题满分高☆考♂资♀源*网12分）
设函数
。
（1）当a=1时，求
的单调区间。
（2）若在
上的最大值为
，求a的值。
【解析】考查函数导数运算、利用导数处理函数最值等知识。
解：对函数求导得：
，定义域为（0，2）
单调性的处理，通过导数的零点进行穿线判别符号完成。
当a=1时，令
当
为增区间；当
为减函数。
区间
上的最值问题，通过导数得到单调性，结合极值点和端点的比较得到，确定
待定量a的值。
当
有最大值，则必不为减函数，且>0，为单调递增区间。
最大值在右端点取到。
。
练习册系列答案
名校课堂系列答案
相关题目
成等差数列。
，其边长
为正整数且
成等差数列。
表示走出迷宫所需的时间。
，抛物线
。
经过
的两个焦点，求
,又M、N为
，且△QMN的重心在
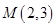射到点
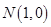后被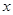
轴反射，求该光线及反射光线所在的直线方程。（请用直线的一般方程表示解题结果）[来源:高&考