题目内容
(不计入总分):已知函数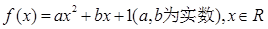 ,设函数
,设函数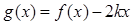 ,
,
(3)当a≠0时,求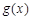 在
在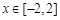 上的最小值
上的最小值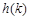 .
.
【答案】
(3)  当
当 时,①当
时,①当 ,即
,即 时,
时, 
②当 ,即
,即 时,
时, 
③当 ,即
,即 时,
时, 
 当
当 时, ①当
时, ①当 ,即
,即 时,
时, 
②当 ,即
,即 时,
时, 
【解析】本试题主要是考查了二次函数在给定区间上的最值的求解。根据定义域和对称轴的位置关系,需要分为三种情况来讨论,并根据单调性,得到最值的求解。
 当
当 时,
时,  图象满足:对称轴:
图象满足:对称轴: 且开口向上
且开口向上
①当 ,即
,即 时,
时, 
②当 ,即
,即 时,
时, 
③当 ,即
,即 时,
时, 
 当
当 时,
时,  图象满足:对称轴:
图象满足:对称轴: 且开口向下
且开口向下
①当 ,即
,即 时,
时, 
②当 ,即
,即 时,
时, 

练习册系列答案
相关题目
 某市教育局规定:初中升学须进行体育考试,总分30分,成绩计入初中毕业升学考试总分,还将作为初中毕业生综合素质评价“运动和健康”维度的实证材料.为了解九年级学生的体育素质,某校从九年级的六个班级共420名学生中按分层抽样抽取60名学生进行体育素质测试.
某市教育局规定:初中升学须进行体育考试,总分30分,成绩计入初中毕业升学考试总分,还将作为初中毕业生综合素质评价“运动和健康”维度的实证材料.为了解九年级学生的体育素质,某校从九年级的六个班级共420名学生中按分层抽样抽取60名学生进行体育素质测试.
