题目内容
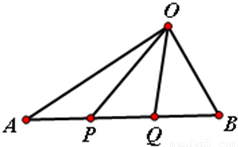
 如图,有以下命题:设P、Q是线段AB的三等分点,则有O
如图,有以下命题:设P、Q是线段AB的三等分点,则有O| P |
| Q |
| A |
| B |
| A1 |
| A2 |
| A3 |
| AN-1 |
| n-1 |
| 2 |
| n-1 |
| 2 |
| A |
| B |
分析:受:“命题:设P、Q是线段AB的三等分点,则有O
+O
=O
+O
”的启示,如果点A1,A2,A3,…,An-1是AB的n(n≥3)等分点,归纳得出猜想O
+O
+O
+…O
=
(O
+O
).再利用向量的运算证明结论.
| P |
| Q |
| A |
| B |
| A1 |
| A2 |
| A3 |
| AN-1 |
| n-1 |
| 2 |
| A |
| B |
解答:解:设
=a,
=b,能得到的结论是:
+
+…+
═
+
.
证明:
∵
=
-
=
-
(
-
)=
+
,
=
-
=
-
(
-
)=
+
,
…
=
-
=
-
(
-
)=
+
,
∴
+
+…+
=(
+
+…+
)
+(
+
+…+
)
=
+
.
故答案为:
.
| OA |
| OB |
| OA1 |
| OA2 |
| OAn-1 |
| n-1 |
| 2 |
| a |
| n-1 |
| 2 |
| b |
证明:
∵
| OA1 |
| OA |
| A1A |
| a |
| 1 |
| n |
| a |
| b |
| n-1 |
| n |
| a |
| 1 |
| n |
| b |
| OA2 |
| OA |
| A2A |
| a |
| 2 |
| n |
| a |
| b |
| n-2 |
| n |
| a |
| 2 |
| n |
| b |
…
| OAn-1 |
| OA |
| An-1A |
| a |
| n-1 |
| n |
| a |
| b |
| 1 |
| n |
| a |
| n-1 |
| n |
| b |
∴
| OA1 |
| OA2 |
| OAn-1 |
| n-1 |
| n |
| n-2 |
| n |
| 1 |
| n |
| a |
| n-1 |
| n |
| n-2 |
| n |
| 1 |
| n |
| b |
=
| n-1 |
| 2 |
| a |
| n-1 |
| 2 |
| b |
故答案为:
| n-1 |
| 2 |
点评:本题考查类比推理、向量加法、减法的运算法则和几何意义,并且运用等差数列求和公式进行计算化简以及进行合情推理.

练习册系列答案
相关题目
 如图,有以下命题:设P、Q是线段AB的三等分点,则有
如图,有以下命题:设P、Q是线段AB的三等分点,则有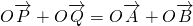 把此命题推广,设点A1,A2,A3…An-1是线段AB的n等分点(n≥3,n∈N*),则有
把此命题推广,设点A1,A2,A3…An-1是线段AB的n等分点(n≥3,n∈N*),则有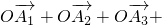 …
…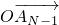 =________(
=________(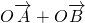 ).
). 把此命题推广,设点A1,A2,A3…An-1是线段AB的n等分点(n≥3,n∈N*),则有
把此命题推广,设点A1,A2,A3…An-1是线段AB的n等分点(n≥3,n∈N*),则有 …
… = (
= ( ).
).
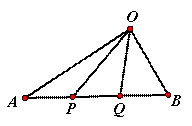 如图,有以下命题:设P、Q是线段AB的三等分点,则有
如图,有以下命题:设P、Q是线段AB的三等分点,则有 如图,有以下命题:设P、Q是线段AB的三等分点,则有
如图,有以下命题:设P、Q是线段AB的三等分点,则有