题目内容
已知直线l: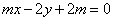 (m
(m R)和椭圆C:
R)和椭圆C: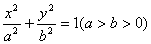 , 椭圆C的离心率为
, 椭圆C的离心率为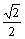 ,连接椭圆的四个顶点形成四边形的面积为2
,连接椭圆的四个顶点形成四边形的面积为2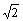 .
.
⑴求椭圆C的方程;
⑵直线l/与椭圆C有两个不同的交点,求实数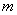 的取值范围;
的取值范围;
⑶当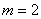 时,设直线l与y轴的交点为P,M为椭圆C上的动点,求线段PM长度的最大值。
时,设直线l与y轴的交点为P,M为椭圆C上的动点,求线段PM长度的最大值。
解:⑴由离心率 ,得
,得
又因为 ,所以
,所以 ,
,
即椭圆标准方程为 . ---------4分
. ---------4分
⑵ 由  消
消 得:
得: .
.
所以 , 可化为
, 可化为 
解得 . --------8分
. --------8分
⑶由l: ,设x=0, 则y=2, 所以P(0, 2). --------9分
,设x=0, 则y=2, 所以P(0, 2). --------9分
设M(x, y)满足 ,
,
则|PM|2 =x2 +(y –2)2 =2–2y2 +(y – 2 )2 = –y2 –4y +6
= –(y +2)2 +10,
因为 –1 y
y 1, 所以 --------11分
1, 所以 --------11分
当y=-1时,|MP|取最大值3 --------14分

练习册系列答案
相关题目
 、
、 、
、 ,则三人中至少有一人达标的概率是 .
,则三人中至少有一人达标的概率是 .
 ,若函数
,若函数 有三个零点,则实数k的取值范围是
有三个零点,则实数k的取值范围是 B.
B.  C.
C.  D.
D. 
 的圆心
的圆心 ,且与直线
,且与直线 垂直的直线方程是( ) A.
垂直的直线方程是( ) A. B.
B. C.
C. D.
D. 
 (
( 为自然对数的底数)的图象相切的直线方程为
为自然对数的底数)的图象相切的直线方程为  中,如
中,如 果
果 ,
, ,则数列
,则数列 的函数
的函数 满足
满足 ,当
,当 时,
时, 若当
若当 时,函数
时,函数 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( ) (B)
(B) (C)
(C) (D)
(D)
 和
和 ,则
,则 的值为 .
的值为 .