题目内容
20.若直线2ax-by+2=0(a>b>0)始终平分圆x2+y2+2x-4y+1=0的周长,则$\frac{1}{a}$+$\frac{1}{b}$的最小值是4,此时a=$\frac{1}{2}$.分析 由题意知,直线过圆心,即-2a-2b+2=0,即a+b=1,再将a+b=1代入所求关系式,利用基本不等式即可求得答案.
解答 解:由于直线2ax-by+2=0(a,b>0),始终平分圆x2+y2+2x-4y+1=0的周长,
故直线2ax-by+2=0必过x2+y2+2x-4y+1=0的圆心(-1,2),
则-2a-2b+2=0,即a+b=1,
则$\frac{1}{a}$+$\frac{1}{b}$=($\frac{1}{a}$+$\frac{1}{b}$)(a+b)=2+$\frac{b}{a}$+$\frac{a}{b}$≥2+2$\sqrt{\frac{b}{a}•\frac{a}{b}}$=4,
当且仅当a=b=$\frac{1}{2}$时,取得最小值4.
故答案为:4,$\frac{1}{2}$.
点评 本题考查直线和圆的位置关系,考查基本不等式的运用,将a+b=1代入所求关系式是关键,属于基础题.

练习册系列答案
相关题目
8.已知0<α<$\frac{π}{2}$,则sinα,α,tanα的大小关系为( )
| A. | tanα>sinα>α | B. | α>tanα>sinα | C. | sinα>α>tanα | D. | tanα>α>sinα |
9.设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)与抛物线y2=8x有一个公共的焦点F,两曲线的一个交点为M.若|MF|=5,则椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
10.下列图象表示的函数中,不能用二分法求零点的是( )
| A. |  | B. | 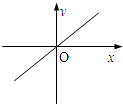 | C. |  | D. | 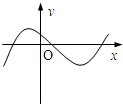 |