题目内容
5.函数y=x+$\frac{a}{x}$(a>0)在(0,+∞)上的增区间是($\sqrt{a}$,+∞).分析 求导y′=1-$\frac{a}{{x}^{2}}$=$\frac{(x-\sqrt{a})(x+\sqrt{a})}{{x}^{2}}$,从而由导数的正负确定函数的单调增区间.
解答 解:∵y=x+$\frac{a}{x}$(a>0),
∴y′=1-$\frac{a}{{x}^{2}}$=$\frac{(x-\sqrt{a})(x+\sqrt{a})}{{x}^{2}}$,
∴当x>$\sqrt{a}$时,y′>0,
故函数y=x+$\frac{a}{x}$(a>0)在(0,+∞)上的增区间是($\sqrt{a}$,+∞);
故答案为:($\sqrt{a}$,+∞).
点评 本题考查了导数的综合应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.将120°化为弧度为( )
| A. | $-\frac{2π}{3}$ | B. | $-\frac{5π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
20.若直线2ax-by+2=0(a>b>0)始终平分圆x2+y2+2x-4y+1=0的周长,则$\frac{1}{a}$+$\frac{1}{b}$的最小值是4,此时a=$\frac{1}{2}$.
17.已知正项等比数列{an}满足:a7=a6+2a5,若存在两项am,an使得$\sqrt{{a_m}{a_n}}=32{a_1}$,则$\frac{1}{m}$+$\frac{4}{n}$的最小值为( )
| A. | $\frac{2}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{5}{6}$ | D. | $\frac{3}{4}$ |
14.已知$\overrightarrow{a}$=(2,0,2),$\overrightarrow{b}$=(-1,-1,0),则错误的是( )
| A. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | B. | <$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{2π}{3}$ | ||
| C. | $\overrightarrow{a}$在$\overrightarrow{b}$上的射影为-$\sqrt{2}$ | D. | $\overrightarrow{b}$在$\overrightarrow{a}$上的射影为-$\frac{\sqrt{2}}{2}$ |
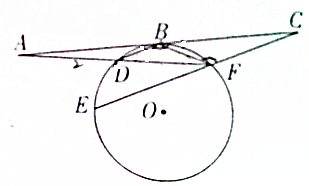 已知直线AC与⊙O相切于点B,AD交⊙O于F、D两点,CF交⊙O于E、F,BD∥CE,AB=BC,AD=2,BD=1
已知直线AC与⊙O相切于点B,AD交⊙O于F、D两点,CF交⊙O于E、F,BD∥CE,AB=BC,AD=2,BD=1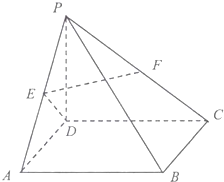 如图,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PD⊥底面ABCD,PD=DA,E、F分别为PA、PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PD⊥底面ABCD,PD=DA,E、F分别为PA、PC的中点.