题目内容
已知函数 ,
, ,若在区间
,若在区间 内,函数
内,函数 与
与 轴有3个不同的交点,则实数
轴有3个不同的交点,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
C
解析试题分析:∵ ,∴
,∴ ,∴
,∴ ,∴
,∴ ,
,
∴ ,∴当
,∴当 时,
时, ,∵函数
,∵函数 与x轴有3个不同交点,∴函数
与x轴有3个不同交点,∴函数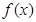 与
与 有3个不同的交点,
有3个不同的交点,
函数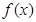 的图像如图所示,直线
的图像如图所示,直线 与
与 相切是一个边界情况,直线
相切是一个边界情况,直线 过
过 时是一个边界情况,符合题意的直线需要在这2条直线之间,
时是一个边界情况,符合题意的直线需要在这2条直线之间,
∵ ,∴
,∴ ,∴
,∴ ,所以切线方程为
,所以切线方程为 ,与
,与 相同,即
相同,即 ,当
,当 过点
过点 时,
时, ,
,
综上可得: ,故选C.
,故选C.
考点:1.导数的运算;2.函数图像;3.曲线的切线.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
若函数 在区间
在区间 上存在一个零点,则
上存在一个零点,则 的取值范围是( )
的取值范围是( )
A. | B. 或 或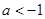 | C. | D.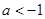 |
函数 的图象( )
的图象( )
| A.关于x轴对称 | B.关于y轴对称 |
| C.关于原点对称 | D.关于直线y x对称 x对称 |
.函数 为偶函数,且在
为偶函数,且在 单调递增,则
单调递增,则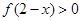 的解集为( )
的解集为( )
A. | B. |
C. | D. |
下列函数是奇函数的是( )
A. | B. |
C. | D. |
设 是
是 上的奇函数,且
上的奇函数,且 时,
时, ,对任意
,对任意 ,不等式
,不等式 恒成立,则
恒成立,则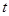 的取值范围( )
的取值范围( )
A. | B. | C. | D. |
若函数 的导函数在区间
的导函数在区间 上的图像关于直线
上的图像关于直线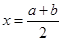 对称,则函数
对称,则函数 在区间
在区间 上的图象可能是( )
上的图象可能是( )
| A.①④ | B.②④ | C.②③ | D.③④ |
已知减函数 是定义在
是定义在 上的奇函数,则不等式
上的奇函数,则不等式 的解集为( )
的解集为( )
A. | B. | C. | D. |
已知f(x)是定义在实数集R上的增函数,且f(1)=0,函数g(x)在(-∞,1]上为增函数,在[1,+∞)上为减函数,且g(4)=g(0)=0,则集合{x|f(x)g(x)≥0}等于( )
| A.{x|x≤0或1≤x≤4} |
| B.{x|0≤x≤4} |
| C.{x|x≤4} |
| D.{x|0≤x≤1或x≥4} |