题目内容
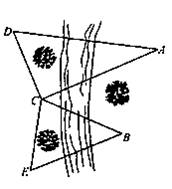
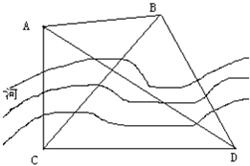
如图,为了测量河对岸A,B两点间的距离,在河的这边测得CD=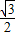 km,∠ADB=∠CDB=30°,∠ACD=60°,∠ACB=45°,A、B两点间的距离为 .
km,∠ADB=∠CDB=30°,∠ACD=60°,∠ACB=45°,A、B两点间的距离为 .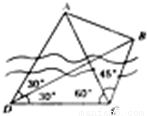
【答案】分析:根据题中条件先分别求出∠DAC,∠DBC.在△ADC中由正弦定理求得AD,在△CDB中由正弦定理求得DB,最后△ADB中由余弦定理求得AB.
解答:解:∠DAC=180°-∠ADB-∠BDC-∠ACD=60°,CD=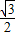 km
km
∴AC=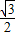 ,
,
∠DBC=180°-∠BDC-∠ACD-∠ACB=45°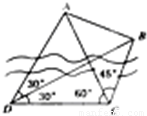
在△CDB中由正弦定理得: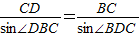
∴BC=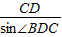 sin∠DBC=
sin∠DBC=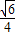
在△ABC中由余弦定理得:AB2=CB2+AC2-2CB•ACcos∠ACB=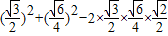 =
=
∴AB=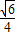 km
km
答:A、B两点间的距离为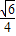 km
km
点评:本题主要考查正弦定理和余弦定理在实际中的应用.由于图象中三角形比较多,应分清在哪个三角形中利用正弦定理和余弦定理.
解答:解:∠DAC=180°-∠ADB-∠BDC-∠ACD=60°,CD=
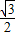 km
km∴AC=
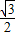 ,
,∠DBC=180°-∠BDC-∠ACD-∠ACB=45°

在△CDB中由正弦定理得:
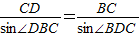
∴BC=
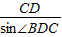 sin∠DBC=
sin∠DBC=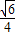
在△ABC中由余弦定理得:AB2=CB2+AC2-2CB•ACcos∠ACB=
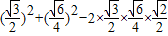 =
=
∴AB=
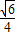 km
km答:A、B两点间的距离为
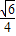 km
km点评:本题主要考查正弦定理和余弦定理在实际中的应用.由于图象中三角形比较多,应分清在哪个三角形中利用正弦定理和余弦定理.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
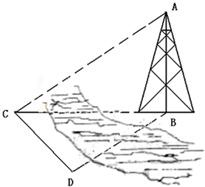 如图,为了测量河对岸的塔高AB,可以选与塔底B在同一水平面内的两个测量点C与D.现测得∠BCD=53°,∠BDC=60°,CD=60(米),并在点C测得塔顶A的仰角为∠ACB=29°,求塔高AB(精确到0.1米).
如图,为了测量河对岸的塔高AB,可以选与塔底B在同一水平面内的两个测量点C与D.现测得∠BCD=53°,∠BDC=60°,CD=60(米),并在点C测得塔顶A的仰角为∠ACB=29°,求塔高AB(精确到0.1米).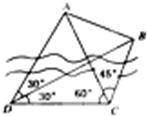 如图,为了测量河对岸A,B两点间的距离,在河的这边测得CD=
如图,为了测量河对岸A,B两点间的距离,在河的这边测得CD= 如图,为了测量河对岸A,B两点间的距离,某课外小组的同学在岸边选取C,D两点,测得CD=200m,∠ADC=105°,∠BDC=15°,∠BCD=120°,∠ACD=30°,则A,B两点间的距离是( )
如图,为了测量河对岸A,B两点间的距离,某课外小组的同学在岸边选取C,D两点,测得CD=200m,∠ADC=105°,∠BDC=15°,∠BCD=120°,∠ACD=30°,则A,B两点间的距离是( )