题目内容
利用展开式(a+b)n=
an+
an-1b+
an-2b2+…+
an-rbr+…+
bn(n∈N*)回答下列问题:
(Ⅰ)求(1+2x)10的展开式中x4的系数;
(Ⅱ)通过给a,b以适当的值,将下式化简:
-
+
-…+(-1)n
;
(Ⅲ)把(Ⅱ)中化简后的结果作为an,求
an的值.
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | r n |
| C | n n |
(Ⅰ)求(1+2x)10的展开式中x4的系数;
(Ⅱ)通过给a,b以适当的值,将下式化简:
| C | 0 n |
| ||
| 2 |
| ||
| 22 |
| ||
| 2n |
(Ⅲ)把(Ⅱ)中化简后的结果作为an,求
| 8 |
 |
| n=1 |
分析:(I)利用二项展开式的通项即可求解
(II)根据展开式的特点,考虑令a=1,b=-
即可求解
(III)结合等比数列的求和公式即可求解
(II)根据展开式的特点,考虑令a=1,b=-
| 1 |
| 2 |
(III)结合等比数列的求和公式即可求解
解答:(本小题满分8分)
解:(Ⅰ)因为(1+2x)10=
110×(2x)0+
19×(2x)1+
18×(2x)2+…+
10×(2x)10
所以
16×(2x)4=3360x4,即(1+2x)10的展开式中x4的系数为3360.…(3分)
(Ⅱ)令a=1,b=-
,得
-
+
-…+(-1)n
=(1-
)n=
.…(6分)
(Ⅲ)
=
+
+…+
=
.…(8分)
解:(Ⅰ)因为(1+2x)10=
| C | 0 10 |
| C | 1 10 |
| C | 2 10 |
| C | 10 10 |
所以
| C | 4 10 |
(Ⅱ)令a=1,b=-
| 1 |
| 2 |
| C | 0 n |
| ||
| 2 |
| ||
| 22 |
| ||
| 2n |
| 1 |
| 2 |
| 1 |
| 2n |
(Ⅲ)
| 8 |
 |
| n=1 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 28 |
| 255 |
| 256 |
点评:本题主要考查了二项展开式的通项在求指定项的应用及利用赋值法求解展开式的系数和,注意方法的灵活应用.

练习册系列答案
相关题目
 可看成是以r为自变量的函数f(r),其定义域是{r|r∈N,r≤n}.
可看成是以r为自变量的函数f(r),其定义域是{r|r∈N,r≤n}. ;
; (n∈N*)回答下列问题:
(n∈N*)回答下列问题: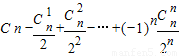 ;
; 的值.
的值. 可看成是以r为自变量的函数f(r),其定义域是{r|r∈N,r≤n}.
可看成是以r为自变量的函数f(r),其定义域是{r|r∈N,r≤n}.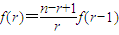 ;
;