题目内容
(满分12分)
如图,在正方体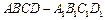 中,E、F、G分别为
中,E、F、G分别为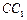 、
、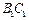 、
、 的中点,O为
的中点,O为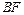 与
与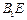 的交点,
的交点,
(1)证明: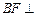 面
面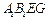
(2)求直线 与平面
与平面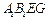 所成角的正弦值.
所成角的正弦值.
如图,在正方体
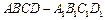 中,E、F、G分别为
中,E、F、G分别为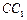 、
、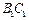 、
、 的中点,O为
的中点,O为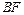 与
与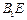 的交点,
的交点,(1)证明:
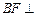 面
面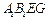
(2)求直线
 与平面
与平面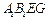 所成角的正弦值.
所成角的正弦值.(1)证明:因为  ,
, ,
,
所以
从而
在 中
中 
故 从而
从而 
即 ………2分
………2分
又因为 ,
, ∥
∥
所以 ………4分
………4分
又因为
故
又因为
所以 ………6分
………6分
(2)解:如右图, 连接
连接

由(1)知,
故 即为直线
即为直线 与平面
与平面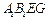 所成角………8分
所成角………8分
设正方体的棱长为1 ,则
 ,
,
在Rt 中,有
中,有  故
故  =
= =
= ………10分
………10分
所以 ………12分
………12分
 ,
, ,
,
所以

从而

在
 中
中 
故
 从而
从而 
即
 ………2分
………2分又因为
 ,
, ∥
∥
所以
 ………4分
………4分又因为

故

又因为

所以
 ………6分
………6分(2)解:如右图,
 连接
连接

由(1)知,

故
 即为直线
即为直线 与平面
与平面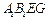 所成角………8分
所成角………8分设正方体的棱长为1 ,则
 ,
,
在Rt
 中,有
中,有  故
故  =
= =
= ………10分
………10分所以
 ………12分
………12分略

练习册系列答案
相关题目
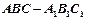 的三视图如图所示,
的三视图如图所示, 其中正视图
其中正视图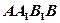 和侧视图
和侧视图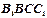 均为矩形,俯视图
均为矩形,俯视图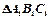 中,
中,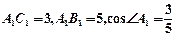 。
。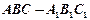 中,求证:
中,求证: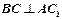 ;
;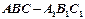 中,若
中,若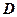 是底边
是底边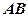 的中点,求证:
的中点,求证: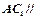 平面
平面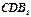 ;
;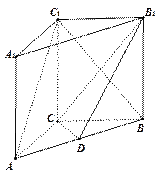
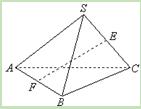
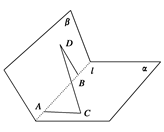
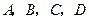 为空间四点.在
为空间四点.在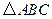 中,
中,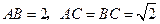 .等
.等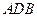 以
以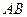 为轴运动.
为轴运动.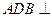 平面
平面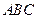 时,求
时,求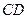 ;
;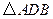 转动时,是否总有
转动时,是否总有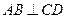 ?证明你的结论.
?证明你的结论.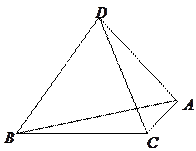
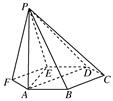
 ,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.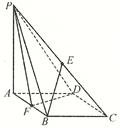
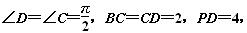 A为PD的中点,如下图,
A为PD的中点,如下图,
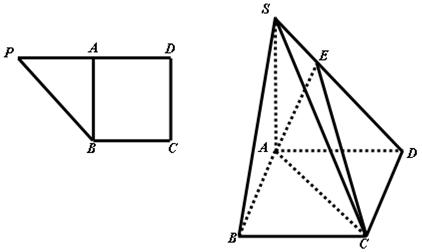
 余弦值;
余弦值; 不存在,请说明理由?
不存在,请说明理由?