题目内容
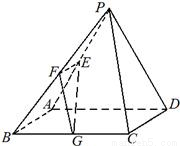
已知一个四棱锥P-ABCD的三视图(正视图与侧视图为直角三角形,俯视图是带有一条对角形的正方形)如下,E是侧棱PC上的动点.(1)求四棱锥P-ABCD的体积;
(2)是否不论点E在何位置都有BD⊥AE,证明你的结论.

分析:(1)根据三视图可知PC⊥面ABCD,从而得到四棱锥P-ABCD的高为PC,底面ABCD是正方形,然后根据四棱锥P-ABCD的体积公式进行求解即可.
(2)是,在任何位置都有BD⊥AE,可证明BD⊥面PAC,根据直线与平面垂直的判定定理可知只需证BD与面PAC内两相交直线垂直,连接AC,则AC⊥BD,PC⊥BD且PC交AC于C点,满足定理所需条件,而E是PC上的动点,所以AE在平面PAC内,从而得到结论.
(2)是,在任何位置都有BD⊥AE,可证明BD⊥面PAC,根据直线与平面垂直的判定定理可知只需证BD与面PAC内两相交直线垂直,连接AC,则AC⊥BD,PC⊥BD且PC交AC于C点,满足定理所需条件,而E是PC上的动点,所以AE在平面PAC内,从而得到结论.
解答:解:(1)由三视图可知,PC⊥面ABCD,且PC=2,
底面ABCD是正方形,故体积Vp-ABCD=
×2×1×1=
;(6分)
(2)是,在任何位置都有BD⊥AE,理由如下:(8分)
连接AC,则AC⊥BD,PC⊥BD且PC交AC于C点,故BD⊥面PAC,
因为E是PC上的动点,所以AE在平面PAC内,所以BD⊥AE不论E在何位置都正确.(12分)
底面ABCD是正方形,故体积Vp-ABCD=
| 1 |
| 3 |
| 2 |
| 3 |
(2)是,在任何位置都有BD⊥AE,理由如下:(8分)
连接AC,则AC⊥BD,PC⊥BD且PC交AC于C点,故BD⊥面PAC,
因为E是PC上的动点,所以AE在平面PAC内,所以BD⊥AE不论E在何位置都正确.(12分)
点评:本题主要考查了三视图与立体图形的转化,以及体积的求解和直线与平面垂直的性质,同时考查了转化与划归的数学思想、计算与推理能力,属于基础题.

练习册系列答案
相关题目
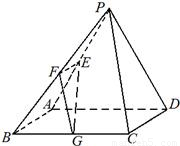
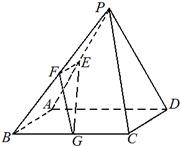 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PA、PB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PA、PB、BC的中点.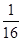 B.
B. C.
C.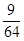 D.
D.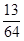
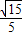 ?
?
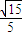 ?
?