题目内容
已知正四棱锥P—ABCD的四条侧棱,底面四条边及两条对角线共10条线段,现有一只蚂蚁沿着这10条线段从一个顶点爬行到另一个顶点,规定: (1)从一个顶点爬行到另一个顶点视为一次爬行;(2)从任一顶点向另4个顶点爬行是等可能的(若蚂蚁爬行在底面对角线上时仍按原方向直行). 则蚂蚁从顶点P开始爬行4次后恰好回到顶点P的概率是( )
A.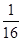 B.
B. C.
C.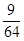 D.
D.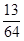
【答案】
D
【解析】
试题分析:第一类:爬行轨迹为PAPAP形式路线,第一步由P到ABCD任意一个都可以,概率为1,第二步回到P的概率为 ,第三步P到ABCD任意一个都可以,概率为1,第四部回到P的概率为
,第三步P到ABCD任意一个都可以,概率为1,第四部回到P的概率为 ,所以概率为
,所以概率为 ,第二类:爬行轨迹为
,第二类:爬行轨迹为 形式路线,第一步由P到ABCD任意一个都可以,概率为1,第二步,第三步的概率均为
形式路线,第一步由P到ABCD任意一个都可以,概率为1,第二步,第三步的概率均为 ,第四部概率为
,第四部概率为 ,所以概率为
,所以概率为
考点:相互独立事件概率
点评:A,B是两个相互事件,则A,B同时发生的概率为 ,本题中要想4次后到达P点需满足第三次不落在P点,因此分了两种情况,第二次到P与不到P
,本题中要想4次后到达P点需满足第三次不落在P点,因此分了两种情况,第二次到P与不到P

练习册系列答案
相关题目
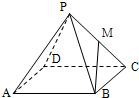
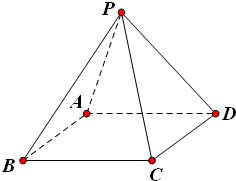 已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
 已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h. ,M是侧棱PC的中点,则异面直线PA与BM所成角为 .
,M是侧棱PC的中点,则异面直线PA与BM所成角为 .