Question

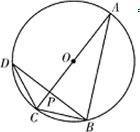①如图，AC为⊙O的直径，弦BD⊥AC于点P，PC=2，PA=8，则cos∠ACB的值为

5

5

．
②若曲线C1：θ=

π

6

（ρ∈R）与曲线C2：

x=a+ 2 cosθ y= 2 sinθ

(θ为参数，a为常数，a＞0）有两个交点A、B，且|AB|=2，则实数a的值为

2

．

Answer 1

分析：①本题考查的知识点是与圆相关的比例线段，由AC为⊙O的直径，弦BD⊥AC于点P，根据射影定理，结合PC=2，PA=8，我们可以求出CD的长，解三角形CDP，即可求出cos∠ACB的值．
②先利用直角坐标与极坐标间的关系，将曲线C₁：θ=

π

6

（ρ∈R）化成直角坐标方程，消去参数将曲线C₂：

x=a+ 2 cosθ y= 2 sinθ

（θ为参数，a为常数，a＞0）化成普通方程，最后利用直角坐标系中直线与圆的位置关系求出其a值即可．

解答：解：①由射影定理得CD²=CP•CA=2×10，
∴CD=2

5

，
则cos∠ACB
=sin∠A
=sin∠D
=

CP

CD

=

2

2 5

=

5

5

．
②曲线C₁：θ=

π

6

（ρ∈R）的直角坐标方程为：x-

3

y=0．
曲线C₂：

x=a+ 2 cosθ y= 2 sinθ

普通方程为：（x-a）²+y²=2．
∵|AB|=2，∴圆心到直线的距离为：1，
即

|a|

1+3

=1，a＞0．
∴a=2．
故答案为：

5

5

； 2

点评：①本小题主要考查圆的有关线段和角，当出现有双垂直情况时，即在直角三角形出现有斜边上的高，我们可以利用射影定理分析边与边的关系．②本小题主要考查简单曲线的极坐标方程、圆的参数方程、直线与圆的位置关系等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题