题目内容

过点P（2，2）作直线l，与两坐标围成三角形面积为8，则这样的直线l有（　　）
A、2条B、1条C、4条D、3条
分析：设直线l的方程为
x
a
+
y
b
=1，把点P（2，2）代入直线l的方程可得
2
a
+
2
b
=1，
又
1
2
|ab|=8，可得
2b+2a=ab
|ab|=16
，解得即可．
解答：解：设直线l的方程为
x
a
+
y
b
=1，
∵点P（2，2）在直线l上，∴
2
a
+
2
b
=1，
∵
1
2
|ab|=8，
∴
2b+2a=ab
|ab|=16
，解得a=b=4或
a=4+4
2
b=4-4
2
或
a=4-4
2
b=4+4
2
．
综上可知：满足条件的直线共有3条．
故选：D．
点评：本题考查了截距式和三角形的面积计算公式，属于基础题．
练习册系列答案
相关题目
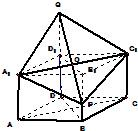精英家教网如图，已知直四棱柱ABCD-A1B1C1D1的底面是边长为2、∠ADC=120°的菱形，Q是侧棱DD1（DD1＞
2
2
）延长线上的一点，过点Q、A1、C1作菱形截面QA1PC1交侧棱BB1于点P．设截面QA1PC1的面积为S1，四面体B1-A1C1P的三侧面△B1A1C1、△B1PC1、△B1A1P面积的和为S2，S=S1-S2．
（Ⅰ）证明：AC⊥QP；
（Ⅱ）当S取得最小值时，求cos∠A1QC1的值．
如图梯形ABCD，AD∥BC，∠A=90°，过点C作CE∥AB，AD=2BC，AB=BC，，现将梯形沿CE折成直二面角D-EC-AB．
（1）求直线BD与平面ABCE所成角的正切值；
（2）设线段AB的中点为P，在直线DE上是否存在一点M，使得PM∥面BCD？若存在，请指出点M的位置，并证明你的结论；若不存在，请说明理由；
（2012•淮南二模）已知椭圆C：
x2
a2
+
y2
b2
=1，（a＞b＞0）与双曲4x2-
4
3
y2=1有相同的焦点，且椭C的离心e=
1
2
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．
（1）求椭圆的方程；
（2）若直MA交直x=4于点P，过P作直线MB的垂线x轴于点Q，Q的坐标；
（3）求点P在直线MB上射R的轨迹方程．
如图梯形ABCD，AD∥BC，∠A=90°，过点C作CE∥AB，AD=2BC，AB=BC，，现将梯形沿CE折成直二面角D-EC-AB．
（1）求直线BD与平面ABCE所成角的正切值；
（2）设线段AB的中点为P，在直线DE上是否存在一点M，使得PM∥面BCD？若存在，请指出点M的位置，并证明你的结论；若不存在，请说明理由；
如图，已知直四棱柱ABCD-A1B1C1D1的底面是边长为2、∠ADC=120°的菱形，Q是侧棱DD1（DD1＞）延长线上的一点，过点Q、A1、C1作菱形截面QA1PC1交侧棱BB1于点P．设截面QA1PC1的面积为S1，四面体B1-A1C1P的三侧面△B1A1C1、△B1PC1、△B1A1P面积的和为S2，S=S1-S2．
（Ⅰ）证明：AC⊥QP；
（Ⅱ）当S取得最小值时，求cos∠A1QC1的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网